CAPITOLUL II

INTRODUCERE ÎN OPTIMIZAREA COMBINATORIALĂ

§ 1. Obiectul optimizării combinatoriale

Combinatorica este un domeniu reprezentativ al matematicilor care, în esenţă, se ocupă cu studiul “aranjamentelor” obiectelor unei mulţimi finite, conforme unei structuri date. În problemele combinatoriale, prioritare sunt chestiunile de existenţă şi de numărare:

· există un anumit tip particular de aranjament?

· câte asemenea aranjamente se pot forma?

Caracteristic problemelor combinatoriale este faptul că numărul acestor aranjamente este finit.

Dacă aranjamentele unei probleme combinatoriale pot fi comparate pe baza unui criteriu de apreciere apare o problemă de optimizare combinatorială:

· care este cel mai bun aranjament din punctul de vedere al criteriului respectiv?

Exemplul 1.1 Să considerăm un graf finit şi simplu G = (V,E) în care V este mulţimea nodurilor iar E este mulţimea muchiilor.Un arbore în graful G este un subgraf H = (V,A) , A Ì E , cu aceleaşi noduri ca şi G, care, de sine stătător, este un graf conex şi fără cicluri (vezi figura 1.1 în care muchiile arborelui au fost îngroşate)

Se pun următoarele chestiuni:

· conţine G cel puţin un arbore?

· câţi arbori distincţi se pot forma?

În cazul de faţă “obiectele de lucru” sunt muchiile

grafului G. Un “aranjament” al acestor obiecte este

o submulţime de muchii A Ì E cu proprietăţile:

· orice nod al grafului G este extremitate pentru cel puţin o muchie din A;

· subgraful H = (V,A) este conex şi fără cicluri.

Următorul rezultat stabileşte în ce condiţii există “aranjamentele” descrise:

Graful G are arbori dacă şi numai dacă este conex.

Amintim doar în treacăt faptul că există o “formulă” care stabileşte numărul arborilor distincţi din G.

Să presupunem mai departe că fiecărei muchii eÎE i s-a asociat un “cost” c(e) ³ 0. Definim costul unui arbore H = (V,A) ca fiind suma costurilor muchiilor alcătuitoare:

Rezultă în final următoarea problemă de optimizare combinatorială a cărei rezolvare va fi prezentată în secţiunea 3:

Să se determine în graful G arborele H^* de cost minim.

Exemplul 1.2 Muchiile grafului G din exemplul 1.1 pot fi aranjate şi în alte moduri. Astfel, un cuplaj în G este o submulţime C Ì E de muchii două câte două neadiacente. Existenţa acestor noi aranjamente este o chestiune banală întrucât orice muchie din G este un cuplaj. Interesante sunt problemele de optimizare care se pun în acest context:

· să se determine cuplajul C^* cu cele mai multe muchii ( cuplajul maxim )

sau, în cazul în care muchiile din G sunt “ponderate”:

· să se determine cuplajul C^* de pondere maximă.

(ca mai sus, ponderea unui cuplaj este dată de suma ponderilor muchiilor din cuplaj)

Este foarte important de menţionat faptul că problemele de optimizare combinatorială provin în marea lor majoritate din diverse domenii de activitate, în special economică: astfel problema arborelui de cost minim din exemplul 1.1 modelează o largă varietate de situaţii practice din domeniul reţelelor de comunicaţii (reţele de calculatoare, de drumuri, televiziune prin cablu etc)

Optimizarea combinatorială are ca obiect rezolvarea problemelor specifice adică elaborarea de metode şi algoritmi de găsire efectivă a celui mai bun “aranjament” din mulţimea finită a tuturor aranjamentelor posibile.În continuare pentru aranjamentele unei probleme combinatoriale vom folosi termenul de soluţie.

La prima vedere, s-ar părea că obiectul optimizării combinatoriale este banal: “Ce mare lucru este să găseşti “cel mai bun” element dintr-o mulţime finită?”

În realitate, listarea tuturor soluţiilor unei probleme combinatoriale, în vederea selectării soluţiei optime, este aproape imposibil de făcut deoarece numărul lor, deşi finit, este de regulă astronomic de mare chiar şi în cazul unor probleme de “talie moderată”.

Exemplul 1.3 Pentru a înţelege mai bine despre ce este vorba să considerăm o altă problemă tipică de optimizare combinatorială, problema comisvoiajorului:

Un comisvoiajor situat în localitatea 0 trebuie să viziteze n localităţi 1,2,…,n în final întorcându-se de unde a plecat. Cunoscând distanţele dintre localităţi (sau costurile deplasărilor între localităţi) el doreşte să găsească traseul cu lungimea totală minimă (sau costul total minim). Este clar că numărul total al traseelor posibile este n! , un traseu fiind perfect determinat de ordinea (permutarea) în care vor fi vizitate cele n localităţi. O dată fixată această ordine calculul lungimii (costului) traseului corespunzător este o banală operaţie de adunare a lungimilor (costurilor) tronsoanelor care compun traseul.

În cazul particular a n=20 de localităţi de vizitat, cu un calculator în stare să examineze un miliard de trasee pe secundă, găsirea traseului optim ar dura circa 800 de ani iar dacă, în loc de 20 de localităţi, am avea cu una mai mult, căutarea ar dura în jur de 16800 de ani!!

În lumina acestui exemplu, determinarea efectivă a unui anumit element dintr-o mulţime finită (dar foarte “numeroasă”…) de posibilităţi este o chestiune serioasă: am dori să găsim acest element în timp util şi bineînţeles cu un efort de calcul rezonabil.

În termeni mai precişi, am dori ca timpul de rezolvare a unei asemenea probleme să depindă “polinomial” de dimensiunile problemei.

Pentru unele probleme de optimizare combinatorială acest lucru este posibil; despre aceste probleme vom spune că sunt uşoare. Problema arborelui de cost minim sau problema cuplajului maxim (de pondere maximă) ,descrise în exemplele 1.1 şi 1.2, sunt dovedite a fi probleme uşoare.

Pentru marea majoritate a problemelor combinatoriale, găsirea soluţiei optime în timp polinomial nu este încă posibilă, altfel spus metodele “exacte” cunoscute necesită un timp de rulare care creşte exponenţial o dată cu creşterea dimensiunilor problemei rezolvate. Mai mult există bănuiala că, datorită structurii lor interne, nici nu va fi posibilă vreodată elaborarea unor metode exacte de rezolvare cu “comportament polinomial”!

Din clasa acestor probleme, socotite grele, face parte şi problema comisvoiajorlui din exemplul 1.3.

Din cele de mai sus nu trebuie înţeles că problemele “grele” sunt inabordabile. În dimensiune “relativ moderată” aceste probleme pot fi soluţionate “exact” în timp rezonabil. Folosind metode de căutare din ce în ce mai sofisticate – care exploatează eficient structura combinatorială internă – au putut fi rezolvate cu succes şi probleme de dimensiuni apreciabile.Totuşi, nu se poate spune că aceste metode, oricât de sofisticate ar fi ele, sunt în stare “să facă faţă” oricărei probleme de acelaşi fel şi mai mult, pot avea comportamente radical diferite pe probleme asemănătoare şi de aceeaşi talie.

Având în vedere aceste observaţii, de mare importanţă, mai cu seamă practică, sunt metodele şi algoritmii care determină “în timp polinomial” o soluţie “acceptabilă”(suboptimală). Pentru aceste procedee, numite generic euristici, aprecierea eficacităţii lor va fi dată de “distanţa” dintre soluţia suboptimală şi cea optimă veritabilă! Am putea aprecia că o anumită euristică este “bună” dacă valoarea suboptimală a criteriului de performanţă ar fi, de exemplu, de cel puţin 90% din valoarea optimă!

Câteva modalităţi de rezolvare a problemei comisvoiajorului sunt date în secţiunea 4.

Cele mai multe probleme de optimizare combinatorială sunt modelate cu ajutorul teoriei grafurilor; exemplul1.1 este edificator în acest sens. Mai toate pot fi descrise alternativ prin programe liniare cu variabile întregi, în special bivalente, de unde strânsa legătură dintre optimizarea combinatorială şi programarea în numere întregi.

Exemplul 1.4 Reluăm problema cuplajului maxim din exemplul 1.2. Ataşăm fiecărei muchii eÎE o variabilă booleană x_e cu semnificaţia:

Pentru fiecare nod vÎ V, fie E(v) mulţimea muchiilor din G care au o extremitate în v. Problema cuplajului maxim este perfect descrisă de programul bivalent:

§ 2. Domenii de aplicare ale optimizării combinatoriale

Între problemele de optimizare combinatorială se găsesc:

· problema drumului de valoare minimă între două noduri ale unui graf;

· problema fluxului maxim;

· problema de afectare.

deja studiate în cursul “Bazele Cercetării Operaţionale” [10]. Ele intră, alături de problema arborelui de cost minim în categoria problemelor uşoare.

Lista problemelor grele este impresionantă şi se îmbogăţeşte continuu. În afara problemei comisvoiajorului mai putem aminti următoarele probleme mai reprezentative:

2.1 Problema croirii În multe domenii cum ar fi industria mobilei, a sticlei, a hârtiei, a confecţiilor, industria metalurgică apar frecvent probleme de debitare (sau croire) a unor repere din suporţi mai mari. Importanţa economică a acestor probleme rezidă în dependenţa directă a reducerii consumului de materiale de utilizarea unor scheme eficiente de croire.

De obicei, clasificarea problemelor de croire se face după dimensiunile relevante ale reperelor: avem probleme unidimensionale, bidimensionale sau tridimensionale. În croirea unidimensională de care ne vom ocupa mai mult, reperele se diferenţiază printr-o singură dimensiune chiar dacă ele au mai multe. Cazul tipic este ecela al debitării unor bare de difrite lungimi din bare mai mari.Iată şi o situaţie concretă: o firmă produce un carton special în rulouri având o anumită lăţime. Clienţii solicită rulouri având aceeaşi lungime ca şi ruloul standard dar de lăţimi mai mici. În acest caz reperele ca şi suporţii sunt bidimensionali dar relevantă este o singură dimensiune – lăţimea.

Aspectul combinatorial al unei probleme de croire este dat de modalităţile de tăiere ale unui suport în repere, modalităţi numite reţete de croire.Chestiunea de optimizare constă în a determina de câte ori una sau alta dintre reţetele de croire trebuie folosită pentru producerea unor cantităţi specificate de repere astfel încât numărul total de suporţi consumaţi să fie minim.

Problema de croire unidimensională va f studiată mai în amănunt în secţiunea 6 din capitolul III.

2.2 Problema generală a ordonanţării Elementele primare sunt:

· o mulţime de utilaje;

· o mulţime de repere (joburi) de realizat (îndeplinit).

Realizarea unui reper necesită efectuarea unei secvenţe de operaţii pe (unele din) utilajele date.Ordinea de parcurgere a utilajelor poate fi aceeaşi pentru toate reperele sau poate diferi de la un reper la altul.Fiecare operaţie necesită un anume timp, presupus cunoscut, şi două operaţii distincte, executabile pe un acelaşi utilaj, nu pot fi programate simultan.Uneori pentru unele repere sunt impuse termene de livrare.

În aceste ipoteze,cum trebuie organizată lansarea reperelor în execuţie astfel încât:

· timpul total de inactivitate al utilajelor să fie minim

· durata de execuţie a tuturor reperelor să fie minimă

· numărul reperelor al căror termen de livrare este depăşit să fie cât mai mic etc.

Există o mare varietate de tipuri de probleme de ordonanţare care se înscriu în acest enunţ general. Modelarea lor - prin programare în numere întregi sau prin grafuri - este în general dificilă, ca să nu mai vorbim de rezolvarea lor "exactă", imposibil de realizat în timp rezonabil, chiar şi atunci când numărul reperelor şi al utilajelor este relativ mic. Ca urmare, au fost elaborate euristici de rezolvare suboptimală, marea lor diversitate fiind explicată prin aceea că ele încearcă să exploateze particularităţile structurii acestor probleme, particularităţi care pot să difere radical de la o problemă la alta.

Unele cazuri particulare vor fi studiate în secţiunea 5 a acestui capitol.

2.3 Problema alegerii traseelor O firmă trebuie să satisfacă un număr de cereri de aprovizionare într-o anumită perioadă. Livrările se fac de la un anumit depozit şi sunt operate cu mai multe de mijloace de transport, fiecare cu o capacitate limitată. Fiecare vehicul pleacă încărcat de la depozit, vizitează unul sau mai mulţi clienţi, cărora le livrează comenzile făcute după care, complet descărcat, se întoarce la depozit pentru a fi eventual reîncărcat. Problema care se pune în acest context este aceea de a stabili traseele de vizitare ale clienţilor astfel încât distanţa totală parcursă de vehicule să fie minimă.

O posibilitate de rezolvare suboptimală este descrisă în secţiunea 6 din acest capitol.

2.4 Problema orariilor Într-o universitate trebuie programată activitatea de învăţământ pe următorul semestru. Se cunosc:

· numărul cursurilor care trebuie ţinute;

· numărul claselor disponibile;

· profesorii abilitaţi să ţină cursurile.

Cum trebuie făcută repartizarea profesorilor pe cursuri şi a cursurilor pe clase astfel încât:

· două cursuri diferite să nu fie programate în aceeaşi clasă şi în acelaşi timp;

· cursurile să fie atribuite profesorilor de specialitate;

· doi profesori cu aceeaşi specialitate să nu fie repartizaţi pe acelaşi curs.

O asemenea repartizare complexă se numeşte orar şi până aici s-a formulat doar o problemă de existenţă. "Optimizarea" elaborării unui orar este o chestiune delicată existând multe criterii de apreciere care nu întotdeauna sunt concordante. Din punctul de vedere al studenţilor un orar este "bun" dacă minimizează totalul deplasărilor zilnice de la o clasă la alta. Atât pentru studenţi cât şi pentru profesori contează numărul "ferestrelor" adică al intervalelor de timp dintre două activităţi zilnice consecutive care ar trebui să fie cât mai mic, etc.

2.5 O problemă de comunicaţii prin satelit Zilnic, un mare volum de informaţii TV, radio sau telefon se transmite prin sateliţi. Utilizarea sateliţilor a devenit imperios necesară pentru asigurarea transmiterii informaţiilor la mare distanţă. În mare, un satelit de comunicaţii este un "releu": el preia semnalul unei staţii terestre de emisie şi îl retransmite altei staţii, de recepţie.Dispozitivul de la bordul satelitului care realizează legătura dintre cele două staţii se numeşte transponder sau conector; sateliţii moderni au până la 24 de conectoare. Una din tehnologiile avansate de operare a sistemelor de comunicaţii prin satelit este SS/TDMA (satellite switched time division multiple access) ; în cadrul acesteia fiecare conector de la bordul satelitului este atribuit - pentru un interval de timp - unei perechi de zone terestre (staţii de emisie - recepţie). Un set complet de atribuiri se va numi în continuare mod de conectare. Atribuirile ce compun un mod de conectare se efectuează simultan de la bordul satelitului. O secvenţă de moduri de conectare care permite realizarea unui program de legături pe o perioadă de timp se numeşte structură de conectare.

O problemă importantă care apare în legătură cu tehnologia SS/TDMA este planificarea eficientă în timp a momentelor de realizare ale atribuirilor ce compun o structură de conectare.

Trecem acum la formalizarea problemei. "Cererea" corespunzătoare unei structuri de conectare poate fi reprezentată printr-o matrice:

D = [d_ij] 1£ i,j £ n

numită matrice de trafic unde:

n º numărul total de zone terestre între care trebuie realizate legăturile;

d_ijº "lungimea" trenului de date necesar a fi transmis din zona i în zona j, lungime exprimată de regulă prin timpul necesar transmiterii trenului de date respectiv.

Transmiterea acestor date implică o programare în timp a conectorilor de pe satelit pe diferite perechi de zone. Aceasta înseamnă descompunerea matricii de trafic D într-un număr de matrici de aceeaşi dimensiune cu ea, numite matrici de conectare:

cu următoarele proprietăţi:

· pe fiecare rând sau coloană din D^k există cel mult un element nenul (altfel spus, în D^k există cel mult n elemente nenule, oricare două nesituate pe acelaşi rând sau coloană. Aceasta revine la a spune că fiecare conector este atribuit la cel mult o pereche de zone;

· suma celor q matrici de conectare este egală cu matricea de trafic dată:

Rezultă imediat că descompunerea matricii D în matrici cu proprietăţile de mai sus este posibilă numai dacă q ³ n.

Criteriul de performanţă ce trebuie avut în vedere în primul rând este transmiterea datelor între diferitele zone în timpul cel mai scurt. Este clar că timpul necesar transmiterii datelor corespunzătoare unui mod de conectare este dat de cea mai mare componentă a matricii de conectare aferente, astfel că timpul total asociat descompunerii (D¹,D²,...,D^q) este:

Cu aceste pregătiri se obţine următoarea problemă de optimizare combinatorială:

Să se determine o descompunere (D¹,D²,...,D^q) a matricii de trafic D în matrici de conectare astfel încât timpul total de transmisie T să fie minim.

Se observă că dacă q > n anumite trenuri de date d_ij din D vor fi fragmentate şi transmise pe parcursul mai multor moduri de conectare. Impunând condiţia ca fiecare tren de date să fie transmis într-un singur mod de conectare rezultă problema:

Să se descompună matricea de trafic D în n matrici de conectare D¹,D²,...,Dⁿ

astfel încât timpul total de transmisie T să fie minim.

§ 3. Problema arborelui de cost minim

Dată în secţiunea 1 ca un prim exemplu de problemă de optimizare combinatorială, problema arborelui de cost minim are numeroase aplicaţii practice. Contextul general este următorul: un număr de “puncte” trebuie conectate între ele pentru facilitarea transmiterii unui anumit serviciu (telefon, TV, calculator) Între puncte există “legături potenţiale” a căror realizare implică un anumit cost. Problema care apare este aceea de a vedea ce legături vor fi efectiv realizate stfel încât:

· oricare două puncte să fie conectate – direct sau indirect – în vederea utilizării serviciului;

· suma costurilor legăturilor realizate să fie minimă.

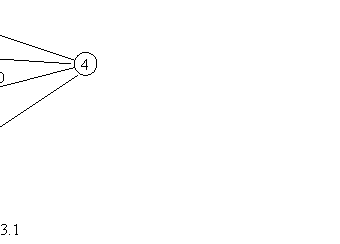
Exemplul 3.1 [6] Centrul regional de calculatoare X trebuie să instaleze un număr de linii speciale de comunicaţii care să lege cinci utilizatori la un nou computer. Deoarece instalarea reţelei este costisitoare conducerea centrului doreşte ca lungimea totală a liniilor instalate să fie cât mai mică. Deşi computerul central poate fi conectat direct cu toţi utilizatorii ar fi mai economic să fie instalate linii directe doar către unii, ceilalţi intrând în reţea prin legarea lor la utilizatorii deja conectaţi.Reţeaua legăturilor posibile este vizualizată prin graful din fig 3.1. Valorile numerice înscrise pe muchii reprezintă distanţe în km.

Exemplul 3.2 Prefectura judeţului X şi-a fixat ca obiectiv modernizarea reţelei drumurilor care leagă între ele localităţile 1,2,…,8 reţea vizualizată în fig. 3.2. Pe fiecare muchie este înscrisă o valoare numerică reprezentând costul modernizării tronsonului respectiv (în milioane lei). Din cauza bugetului limitat, prefectura doreşte ca într-o primă etapă să modernizeze numai unele drumuri astfel încât:

· între oricare două localităţi să se poată circula pe tronsoane modernizate;

· costul întregii operaţii de modernizare parţială să fie minim.

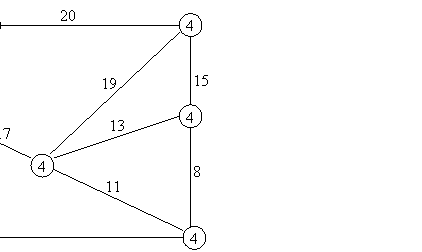
Figura 3.2

Rezolvarea problemelor de acest tip se face cu ajutorul unui algoritm foarte simplu, datorat lui Kruskal:

· selectarea muchiilor care vor forma arborele căutat se va face în ordinea crescătoare a costurilor;

· presupunând că muchiile e₁ , e₂ ,…, e_k au fost deja selectate, următoarea muchie e_{k + 1} va fi astfel aleasă încât să nu formeze ciclu cu (unele din) muchiile e₁ , e₂ ,…, e_k.

Este clar că procedura se opreşte după un număr finit de paşi. Dacă numărul total de muchii selectate este n – 1, n fiind numărul nodurilor din graful original, s-a găsit un arbore de cost minim; altminteri, graful dat nu este conex!

Exemplul 3.3 Vom aplica algoritmul lui Kruskal în graful conex din fig. 3.1. Există trei muchii cu costul minim 20;ele nu formează un ciclu astfel că ele pot fi selectate în orice ordine, de exemplu: {0,1} , {2,3} , {2,5}. Mai departe a fost aleasă muchia {0,3} urmată de {3,4}; muchia {3,5}a fost respinsă deoarece forma un ciclu cu muchiile {2,3} şi {2,5} deja selectate! Procedura s-a oprit deoarece graful are şase noduri şi au fost alese cinci muchii.Arborele cu costul minim 120 este reprezentat în fig.3.3

Figura 3.3

§ 4. Problema comisvoiajorului

Un comisvoiajor are de vizitat un număr de oraşe, la sfârşitul voiajului el întorcându-se în localitatea de plecare. Deplasarea dintr-o localitate în alta presupune anumite cheltuieli (sau distanţe de parcurs sau durate de mers).

In ce ordine trebuiesc vizitate oraşele astfel încât costul total al deplasării (sau lungimea traseului sau durata călătoriei) să fie minim?

Astfel enunţată, problema comisvoiajorului (notată pe scurt TSP de la Travelling Salesman Problem) este una din cele mai grele probleme de optimizare combinatorială. Pe lângă importanţa teoretică, ea are numeroase aplicaţii practice. De exemplu, stabilirea celor mai "economice" trasee turistice într-un mare oraş sau zonă istorică (din punctul de vedere al costurilor sau distanţelor) este o probemă a comisvoiajorului. De asemenea, stabilirea ordinii în care un număr de operaţii (joburi) vor fi executate pe un utilaj, astfel încât suma timpilor de pregătire ai utilajului să fie cât mai mică, este o problemă de acelaşi tip.

4.1 Modelul matematic al problemei comisvoiajorului

Să notăm cu 0,1,...,n oraşele problemei, 0 fiind oraşul din care comisvoiajorul pleacă şi în care revine la terminarea călătoriei. Fie c_ij costul deplasării din localitatea i în localitatea j ¹ i; punem c_ij = ¥ dacă nu există legătură directă între i şi j sau în cazul i = j. Un traseu va fi descris cu ajutorul variabilelor bivalente :

Urmează a fi minimizată funcţia:

(4.1.1)

Din orice oraş i, comisvoiajorul trebuie să se îndrepte către o altă localitate, astfel că:

(4.1.2)

In orice oraş ar ajunge, comisvoiajorul vine dintr-o localitate anterior vizitată, aşa că:

(4.1.3)

Observăm că ansamblul (4.1.1) - (4.1.3) constituie modelul matematic (PA) al unei probleme generale de afectare. O examinare mai atentă a problemei arată că restricţiile (4.1.2) şi (4.1.3) nu definesc numai trasee ce trec prin toate oraşele (o singură dată!) ci şi "reuniuni" de circuite disjuncte mai mici! Astfel, într-o problemă cu 7 oraşe 0,1,...,6 ansamblul:

x₀₃ = x₃₅ = x₅₀ = x₂₁ = x₁₄ = x₄₆ = x₆₇ = x₇₂ = 1 , x_ij = 0 în rest

satisface restricţiile (4.1.2) şi (4.1.3) dar nu constituie un traseu complet aşa cum se vede din figura 4.1

Fig. 4.1

Pentru evitarea ecestui neajuns asociem oraşelor 1,2,...,n , diferite de localitatea de plecare şi sosire 0, variabilele y₁,y₂,...,y_n şi introducem inegalităţile:

y_i - y_j + n×x_ij £ n - 1 i , j = 1,2,...,n ; i ¹ j (4.1.4)

In principiu noile variabile pot lua orice valoare reală. Vom arăta că dacă x = (x_ij) determină un traseu complet atunci există valori numerice y₁,y₂,...,y_n care împreună cu x_ij satisfac relaţiile (4.1.4). Intr-adevăr, definim y_i ca fiind numărul de ordine al localităţii i în cadrul traseului determinat de x. Pentru i ¹ j două situaţii sunt posibile:

· localitatea j nu urmează imediat după localitatea i. Atunci x_ij = 0 şi (4.1.4) devine y_i - y_j £ n - 1 ceeace este adevărat având în vedere semnificaţia acordată valorilor y₁,y₂,...,y_n.

· localitatea j urmează imediat după localitatea i. Atunci y_j = y_i+ 1 , x_ij = 1 şi (4.1.4) se verifică cu egalitate.

Să presupunem acum că z = (x_ij) defineşte o reuniune de "subtrasee" disjuncte. Alegem unul care nu trece prin localitatea 0 şi fie k numărul deplasărilor cel compun. Presupunând că ar exista valori numerice y₁,y₂,...,y_n care să satisfacă (4.1.4) însumăm pe acelea corespunzătoare deplasărilor de la un oraş la altul din subtraseul ales. Obţinem n×k £ (n - 1)×k ceeace este evident fals.

In concluzie, ansamblul (4.1.1) - (4.1.4) constituie modelul "corect" al problemei comisvoiajorului. Este vorba de un program mixt ce utilizează atât variabile întregi (bivalente) cât şi variabile care pot lua orice valoare. In continuarea unei observaţii anterioare, putem spune că problema comisvoiajorului (TSP) este o problemă de afectare (PA) (ansamblul (4.1.1) - (4.1.3)) cu restricţiile speciale (4.1.4).

In consideraţiile de mai sus costurile c_ij nu sunt "simetrice" adică este posibil ca c_ij ¹ c_ji. Problema simetrică a comisvoiajorului se caracterizează prin c_ij = c_ji; aceasta se întâmplă dacă , de exemplu, c_ij sunt distanţe sau timpi de parcurgere.

Un caz particular al problemei simetrice este aşa numita problemă euclidiană a comisvoiajorului în care distanţele c_ij satisfac inegalitatea triunghiului :

c_ik £ c_ij + c_jk (") i,j,k.

4.2 Un algoritm exact de rezolvare a problemei comisvoiajorului

Următorul algoritm, de tip B&B, reduce rezolvarea TSP la rezolvarea unei liste de probleme de afectare. El s-a dovedit suficient de robust pentru probleme asimetrice cu un număr moderat de oraşe. Principalul dezavantaj îl reprezintă faptul că numărul problemelor de afectare de rezolvat este impredictibil şi poate fi imens în cazul situaţiilr reale.Algoritmul este datorat lui Eastman. Ca orice procedură de tip B&B, el utilizează:

· o "locaţie" x_CMB care va reţine "cel mai bun" traseu găsit de algoritm până la un moment dat;

· o variabilă z_CMB care reţine costul traseului memorat în x_CMB;

· o listă L de probleme de afectare asemănătoare problemei (PA) şi care diferă de problema (PA) iniţială prin anumite costuri c_ij schimbate în ¥;

La start:

· x_CMB poate fi locaţia "vidă" în care caz z_CMB = ¥ sau reţine un traseu arbitrar ales sau generat printr-o metodă euristică, x_CMB fiind iniţializat cu costul aferent acestui traseu;

· lista L cuprinde numai problema (PA) iniţială, determinată de (4.1.1) - (4.1.3);

Pasul 1. Dacă lista L este vidă Stop. Altminteri, selectează o problemă din lista L . Problema aleasă se şterge din L . Se trece la:

Pasul 2. Se rezolvă problema selectată. Dacă valoarea funcţiei obiectiv este ³ z_CMB se revine la pasul 1. Altminteri, se trece la:

Pasul 3. Dacă soluţia optimă este un traseu complet se actualizează x_CMB şi z_CMB după care se revine la pasul 1. Altminteri se trece la:

Pasul 4. (Soluţia optimă nu este un traseu ci o reuniune de "subtrasee mai mici"). Din soluţia optimă se selectează circuitul cu cel mai mic număr de arce. Pentru fiecare arc (i,j) din circuitul ales (pentru care x_ij = 1) se adaugă la lista L problema obţinută din cea rezolvată punând c_ij = ¥. Se revine la pasul 1.

Observaţii: 1) Raţiunea pasului 4 este clară: dacă i ® j ® k ® ... ® l ® i este circuitul selectat este clar că în traseul optim vom avea:

x_ij = 0 sau x_jk = 0 sau ... sau x_li = 0.

In consecinţă, vom căuta traseul optimal printre cele în care x_ij = 0 şi dacă nu este acolo printre cele în care x_jk = 0 ş.a.m.d. Limitarea la traseele în care x_ij = 0 se face efectuând schimbarea c_ij = ¥.

2) La pasul 4, în lista L vor apare atâtea probleme câte arce are circuitul selectat; de aceea se alege circuitul cu cel mai mic număr de arce!

In raport cu termenii generali ai unei metode B&B, ramificarea are loc la pasul 4 în timp ce mărginirea se efectuează la pasul 2.

Exemplul 4.2.1 Se consideră problema asimetrică a comisvoiajorului cu cinci oraşe, definită de următoarea matrice a costurilor:

Oraşe	0	1	2	3	4
0	¥	10	25	25	10
1	1	¥	10	15	2
2	8	9	¥	20	10
3	14	10	24	¥	15
4	10	8	25	27	¥

Tabelul 4.1

Start. Se pleacă cu traseul 0 ® 1® 2 ® 3 ® 4 ® 0, care se reţine în x_CMB şi al cărui cost este z_CMB = 10 + 10 + 20 + 15 + 10 = 65. Lista L a problemelor de afectare ce urmează a fi rezolvate cuprinde numai problema iniţială (PA).

Iteraţia 1. Se şterge (PA) din lista L şi se rezolvă. Se obţine soluţia optimă:

x₀₄ = x₄₀ =x₁₂ = x₂₃ = x₃₁ = 1,x_ij = 0în rest

ce corespunde reuniunii următoarelor subtrasee:

0 ® 4 ® 0 şi 1 ® 2 ® 3 ® 1

Selectăm subtraseul 0 ® 4 ® 0 şi adăugăm la L problemele PA₁ şi PA₂ derivate din PA înlocuind c₀₄ respectiv c₄₀ cu ¥ .

Iteraţia 2. Selectăm problema PA₁ şi o rezolvăm. Lista L va cuprinde mai departe numai problema PA₂. Pentru PA₁ se găseşte soluţia optimă:

x₀₃ = x₁₂ = x₂₄ = x₃₁ = x₄₀ = 1 , x_ij = 0în rest.

care corespunde traseului complet 0 ® 3 ® 1 ® 2 ® 4 ® 0. Costul său este 65 = z_CMB. Nu am găsit deci un traseu mai bun decât cel pe care-l avem în x_CMB.

Iteraţia 3. Rezolvăm problema PA₂, singura rămasă în L .Se obţine soluţia optimă:

x₀₄ = x₁₂ = x₂₃ = x₃₀ = x₄₁ = 1 , x_ij = 0 în rest

care corespunde traseului 0 ® 4 ® 1 ® 2 ® 3 ® 0 . Costul noului traseu este 62 < z_CMB ,drept care îl reţinem în x_CMB şi actualizăm z_CMB = 62.

Deoarece lista L este acum vidă traseul reţinut în x_CMB este optim.

4.3 Metode euristice de rezolvare aproximativă a problemei comisvoiajorului

De obicei, soluţia optimă a unei TSP este foarte greu de găsit (dacă nu chiar imposibil de găsit) atunci când numărul oraşelor de vizitat este mare (peste 50). Pentru determinarea unei soluţii măcar acceptabile au fost elaborate mai multe procedee euristice. Aceste procedee merită atenţie din două puncte de vedere:

· se poate da un "certificat de garanţie" pentru soluţia obţinută în sensul că este posibilă evaluarea "depărtării" maxime de soluţia optimă;

· soluţia aproximativă este găsită cu un efort de calcul relativ moderat şi într-un timp rezonabil, aceasta însemnând că cei doi parametri depind polinomial de dimensiunea problemei (adică numărul de oraşe);

In multe situaţii practice, procedeele euristice au condus chiar la soluţia optimă dar acest lucru a fost confirmat numai prin aplicarea unui algoritm exact.

In principiu, o metodă euristică construieşte o soluţie prin tatonare, din aproape în aproape, făcând la fiecare pas, cea mai bună alegere posibilă. Din nefericire, această "schemă" nu conduce, de regulă, la cea mai bună alegere globală.

In continuare, vom prezenta mai multe euristici pentru rezolvarea problemei euclidiene a comisvoiajorului, adică a problemei în care c_ij sunt distanţe ce satisfac:

· condiţia de simetrie: c_ij = c_ji:

· inegalitatea triunghiului c_ik £ c_ij+ c_jk;

Euristica E₁ (mergi la cel mai apropiat vecin)

· se pleacă din localitatea 0 către localitatea cea mai apropiată;

· din ultima localitate vizitată se pleacă către cea mai apropiată localitate nevizitată; în caz că nu mai există localităţi nevizitate se revine în locul de plecare;

Exemplul 4.3.1 Să considerăm cele 13 oraşe din reţeaua laticială din figura 4.2; distanţele dintre oraşe sunt date în tabelul 4.2.

Aplicând euristica descrisă se obţine traseul din figura 4.3 cu lungimea 5099.

Figura 4.2 Figura 4.3

Localitatea		0	1	2	3	4	5	6	7	8	9	10	11	12
	0	¥	100	141	360	500	400	1000	1019	1204	806	632	1004	1204
	1		¥	100	282	447	412	1004	1004	1140	721	538	905	1170
	2			¥	223	360	316	905	905	1063	670	509	900	1140
	3				¥	200	360	854	806	860	447	300	707	921
	4					¥	300	670	608	707	400	360	761	900
	5						¥	600	632	943	700	632	1044	1200
	6							¥	200	806	921	1000	1345	1341
	7								¥	608	781	894	1204	1166
	8									¥	509	728	824	640
	9										¥	223	424	500
	10											¥	412	632
	11												¥	360
	12													¥

Tabelul 4.2

Euristica E₂ (Ajustare locală)

· se pleacă de la un traseu complet, determinat fie "la întâmplare" fie printr-o altă euristică;

· se caută două arce (u,v) şi (x,y) ale traseului care se încrucişează - ca în figura 4.4 a) - şi se compară distanţele c_uv + c_xy cu c_ux + c_vy. Dacă c_uv + c_xy > c_ux + c_vy se înlocuiesc arcele (u,v) şi (x,y) cu (u,x) şi (v,y) obţinându-se un traseu de lungime mai mică (vezi figura 4.4 b));

· procedura se opreşte în momentul în care nu mai există situaţii similare cu cea descrisă;

Figura 4.4 a) Figura 4.4 b)

Exemplul 4.3.2 Pentru ilustrare să considerăm traseul obţinut din euristica E₁. In figura 4.3 este vizibilă încrucişarea arcelor (10,11) şi (12,0). Deoarece:

c_10,11 + c_12,0 = 424 +1264 = 1688 > 1636 = 632 + 1004 = c_10,12 + c_11,0

un traseu mai scurt se obţine folosind arcele (10,12) şi (11,0) aşa cum se arată în figura 4.5 a).

a) b)

Figura 4.5

Lungimea noului traseu este: 5099 - (1688 - 1636) = 5047.

Rezolvând analog încrucişarea nou apărută a arcelor (1,2) şi (11,0) - vezi figura 4.5 a) - în care:

c_1,2 + c_11,0 = 100 + 1004 = 1104 > 1046 = 141 + 905 = c_0,2 + c_11,1

se obţine traseul din figura 4.5 b) cu lungimea: 5047 - (1104 - 1046) = 4989.

Deoarece în noul traseu nu mai apar încrucişări euristica E₂ se opreşte.

Următoarele procedee sunt "mai performante" dar necesită şi un efort de calcul "mai mare".

Euristica E₃

· Se determină un arbore H de lungime minimă (aceasta este o problemă "uşoară" rezolvabilă de exemplu cu algoritmul lui Kruskal, vezi seţiunea 3);

· fiecare muchie a arborelui H şe înlocuieşte cu două muchii de aceeaşi lungime. Se obţine un multigraf H' în care fiecare nod are grad par. Conform teoremei lui Euler în H' există un ciclu eulerian; cu alte cuvinte, este posibil să se viziteze oraşele astfel încât fiecare muchie a multigrafului H' să fie parcursă o singură dată.

Fie:

0 ® x ® y ® ¼ ® u ® v ® 0 (4.3.1)

succesiunea în care muchiile multigrafului H' au fost parcurse. Lungimea acestui "traseu" este de două ori mai mare decât lungimea arborelui minimal H. In această secvenţă, unul sau mai multe oraşe apar de mai multe ori. Vom proceda atunci la următoarea operaţie de scurtcircuitare:

· în succesiunea (4.3.1) se determină prima tripletă de oraşe succesiv vizitate

i ® j ® k

cu proprietatea că oraşul j "din mijloc" mai apare ulterior în succesiune. Se înlocuieşte secvenţa i ® j ® k cu arcul i ® k. Prin această scurtcircuitare:

· fiecare oraş continuă să fie vizitat cel puţin o dată;

· noul traseu este mai scurt pentru că c_ij + c_jk ³ c_ik;

Operaţia de scurtcircuitare se repetă până când în secvenţa (4.3.1) "actualizată" fiecare oraş, cu excepţia localităţii 0 apare o singură dată.

Se poate demonstra că lungimea traseului obţinut prin această euristică este cel mult de două ori mai mare decât lungimea traseului optim (în practică lucrurile stau însă mai bine...)

Figura 4.6

Exemplul 4.3.3 In figura 4.6 este vizualizat un arbore minimal H pentru graful din figura 4.2. Un ciclu eulerian în multigraful H', dedus din H prin "dublarea" muchiilor acestuia, arată astfel:

0 ® 1 ® 2 ® 3 ® 4 ® 5 ® 6 ® 7 ® 6 ® 5 ® 4 ® 3 ® 10 ® 9 ® 8 ® 9 ® 10 ® 11 ® 12 ® 11 ® 10 ® 3 ® 2 ® 1 ® 0

În succesiunea 0 ® 1 ® 2 de lungime c₀₁ + c₁₂ = 100 + 100 = 200 oraşul 1 mai este vizitat "în final". Conform celor de mai sus, vom înlocui această succesiune cu arcul direct 0 ® 2 de lungime 141 < 200. Rezultă traseul:

0 ® 2 ® 3 ® 4 ® 5 ® 6 ® 7 ® 6 ® 5 ® 4 ® 3 ® 10 ® 9 ® 8 ® 9 ® 10 ® 11 ® 12 ® 11 ® 10 ® 3 ® 2 ® 1 ® 0

Mai departe succesiunea 0 ® 2 ® 3 de lungime 141 + 223 = 364 se înlocuieşte cu arcul direct 0 ® 3 cu lungimea 360, pentru că prin oraşul 2 se mai trece o dată!

Continuând procesul de scurtcircuitare se obţine în final traseul complet:

0 ® 7 ® 6 ® 5 ® 4 ® 8 ® 9 ® 12 ® 11 ® 10 ® 3 ® 2 ® 1 ® 0

vizualizat în figura 4.7; lungimea sa este 5330. Rezolvând "încrucişarea" arcelor (0,7) şi (5,4) se obţine traseul mai scurt din figura 4.8 cu lungimea 5019.

Figura 4.7 Figura 4.8

Menţionăm faptul că euristica descrisă poate da rezultate diferite, unele mai bune altele mai puţin bune, funcţie de alegerea arborelui minimal H şi a ciclului eulerian în multigraful asociat H'.

Euristica E₄

Această procedură, datorată lui Cristofides, este o rafinare a euristicii precedente. Deoarece suma gradelor nodurilor din arborele H este pară, numărul nodurilor de grad impar este par! Folosind numai aceste noduri şi muchiile dintre ele vom determina cuplajul C de pondere minimă, ponderile muchiilor luate în calcul fiind distanţele dintre extremităţi.

Fie H' graful rezultat din H prin adăugarea muchiilor cuplajului C, cu menţiunea că dacă între două noduri avem o muchie în H şi o alta în C, graful H' va avea între nodurile respective două muchii.Prin construcţie, în H' fiecare nod are grad par, astfel că H' are un ciclu eulerian. Plecând de aici şi utilizând tehnica scurtcircuitării se ajunge la un traseu complet.

Se poate arăta că lungimea acestui traseu nu depăşeşte 3/2 din lungimea traseului optim.

Exemplul 4.3.4 Reluăm problema euclidiană a comisvoiajorului definită în figura 4.2 şi tabelul 4.2. Un arbore minimal cu lungimea 3527 apare în figura 4.6. Nodurile din H de grad impar sunt 0, 3, 7, 8 şi 12. Prin simpla inspecţie (sau utilizând un algoritm de determinare a cuplajului de pondere minimă în subgraful complet ale cărui noduri sunt 0, 3, 7, 8 şi 12) se constată că muchiile {0,3} , {7,8} şi {10,12} au cea mai mică pondere totală: c₀₃ + c₇₈ + c_10,12 = 360 + 608 + 632 = 1600. Adăugând cele trei muchii la arborele H se obţine graful H' din figura 4.9. Vizitând oraşele 0,1,...,12 în ordinea:

0 ® 1 ® 2 ® 3 ® 4 ® 5 ® 6 ® 7 ® 8 ® 9 ®10 ® 11 ® 12 ® 10 ® 3 ® 0

toate muchiile grafului H' vor fi parcurse o singură dată. "Scurtcircuitând" secvenţele 2 ® 3 ® 4 şi 9 ®10 ® 11 se obţine un traseu complet cu lungimea 4853. Invităm cititorul să se convingă prin desen că în acest traseu arcele (9,11) şi (12,10) respectiv (1,2) şi (3,0) se încrucişează. Rezolvând şi aceste încrucişări se obţine în final traseul din figura 4.10 cu lungimea 4672.

Ca şi euristica precedentă şi E₄ poate conduce la rezultate diferite, funcţie de alegerea arborelui minimal H, al cuplajului C şi al ciclului eulerian în (multi)graful H'.

Figura 4.9 Figura 4.10

§ 5. Introducere în problema ordonanţării

5.1 Problema ordonanţării. Aspecte generale

Considerăm un proces tehnologic în care, asupra unor obiecte (materie primă, semifabricate) denumite generic repere, se efectuează o serie de transformări cantitative şi/sau calitative în vederea obţinerii unor produse (acestea pot fi produse finite sau semifabricate mai complexe ce devin repere în alte procese tehnologice). Transformările (prelucrările) pe care le suferă un reper în diferitele faze ale procesului tehnologic se execută pe utilaje specializate. Pentru precizia limbajului vom numi operaţie totalitatea acţiunilor de prelucrare efectuate asupra unui reper pe un anumit utilaj. In principiu, un utilaj poate executa operaţii aferente mai multor repere dar, la un moment dat, nu poate executa decât o singură operaţie.

Efectuarea unei operaţii presupune utilizarea unor resurse materiale sau băneşti; avem în vedere în primul rând durata operaţiei care se "extrage" din fondul de timp productiv al utilajului pe care se execută operaţia respectivă.

In contextul descris, problema ordonanţării reperelor pe utilaje înseamnă programarea în timp a operaţiilor necesare obţinerii diferitelor produse din nomenclatorul procesului tehnologic studiat, adică stabilirea ordinii şi a termenelor la care urmează a fi efectuate aceste operaţii.

In elaborarea unui program concret de lansare în fabricaţie trebuie să se ţină seama de un mare număr de factori cei mai mulţi fiind specifici procesului tehnologic studiat. Vom menţiona pe cei mai importanţi fără pretenţia de epuizare a subiectului.

· Cu puţine excepţii, planificarea nu se referă la repere individualizate ci la loturi de repere. În această situaţie, este posibil ca după ce o anumită operaţie a fost executată pe o parte a unui lot de repere, utilajul să fie eliberat şi pregătit pentru o operaţie ce se efectuează pe reperele altui lot, restul reperelor din lotul anterior urmând a fi prelucrat mai târziu. Deoarece în procesul de modelare un lot de repere identice este asimilat cu un singur reper (dar cu o durată de execuţie proporţională cu mărimea lotului), situaţia descrisă mai sus este echivalentă cu întreruperea unei operaţii şi reluarea ei la un moment ulterior. In consecinţă, lansarea în execuţie a reperelor pe utilaje poate fi concepută cu acceptarea sau neacceptarea ipotezei de întrerupere a operaţiilor.

· Ordinea în care se execută cel puţin unele din operaţiile aferente unui reper este esenţială în foarte multe cazuri practice. Ca şi în analiza drumului critic, condiţionările dintre operaţiile unui reper pot fi complet descrise cu ajutorul relaţiei de precedenţă directă: operaţia a precede direct operaţia b dacă b poate fi executată imediat după terminarea operaţiei a. Putem vizualiza structura tehnologiei de fabricaţie a unui reper printr-un graf orientat ale cărui noduri sunt operaţiile reperului în cauză, arcele reprezentând precedenţele directe dintre operaţii.

Din punctul de vedere al ordinii în care se execută operaţiile, problemele de ordonanţare implicând utilizarea a cel puţin două maşini se clasifică în trei categorii:

1) ordinea în care se execută operaţiile oricărui reper este neesenţială (open shop);

2) toate reperele parcurg utilajele într-o aceeaşi ordine (flow shop);

3) fiecare reper parcurge utilajele într-o anumită ordine definită de tehnologia de fabricaţie a reperului (job shop);

· In practică, pentru orice reper (sau lot de repere) există un termen de predare (livrare) la care toate operaţiile trebuiesc încheiate; în consecinţă, un program concret de lansare în execuţie va fi apreciat ca admisibil dacă operaţiile fiecărui reper sunt încheiate înaintea termenului de predare.

· De cele mai multe ori, pentru a fi siguri că termenele de predare vor fi respectate, planificatorii îşi fixează pentru fiecare reper (sau lot de repere) un termen "intern" de predare care devansează mai mult sau mai puţin, funcţie de specificul situaţiei concrete, termenele de livrare. Există şi alte raţiuni care impun asemenea termene, ca de exemplu eliberarea utilajului la o anumită dată în vederea executării altor comenzi. Aceste termene "interne", denumite de obicei termene impuse, sunt foarte utile în aprecierea diferitelor programe posibile de lansare în execuţie în sensul că un program va fi socotit mai bun decât altul dacă întârzierile faţă de termenele impuse vor fi mai mici fie pe total fie individual.

· Intr-o situaţie concretă, toate programele admisibile de ordonanţare raportează termenele de execuţie ale operaţiilor la un acelaşi moment de referinţă: zero sau o dată calendaristică. Deseori se întâmplă ca unele din utilajele necesare prelucrării reperelor situaţiei să nu fie disponibile la momentul de referinţă, fiind antrenate în executarea altor comenzi. In raport cu momentul de referinţă ales de planificator, fiecare utilaj va avea un termen de eliberare de la care el devine disponibil (accesibil) şi un program viabil (realist) de ordonanţare trebuie să ţină seama de aceste termene.O chestiune similară se pune şi în cazul reperelor care nu întotdeauna sunt disponibile la momentul de referinţă ci la anumite termene minime de lansare în execuţie.

· De obicei, pentru a executa o anumită operaţie, utilajul desemnat trebuie pregătit (reglat). Există cazuri în care timpul de pregătire este apreciabil şi trebuie luat în considerare în elaborarea unui program realist de ordonanţare. Lucrurile se complică foarte mult dacă avem în vedere faptul că timpul de pregătire nu depinde numai de operaţia ce urmează a fi executată ci şi de operaţia anterior executată pe acelaşi utilaj.

· Este posibil ca, pentru executarea unei operaţii, să fie disponibile mai multe utilaje, fie identice, fie neidentice ca performanţă. Este clar că, în al doilea caz, durata efectivă de execuţie a operaţiei depinde de performanţele utilajului desemnat.

Cu toate că lista factorilor restrictivi ar putea fi continuată, situaţiile concrete de ordonanţare implică un număr enorm de programe admisibile. Se impune alegerea unui criteriu de performanţă care să clasifice aceste programe. Criteriile pot diferi de la o situaţie la alta şi chiar pentru una şi aceeaşi situaţie se pot formula criterii independente (care să conducă la soluţii diferite). Vom cita, cu titlu informativ, câteva din criteriile de performanţă ce pot fi avute în vedere:

· minimizarea termenului la care toate operaţiile de prelucrare ale reperelor sunt încheiate;

· minimizarea sumei întârzierilor faţă de termenele impuse;

· minimizarea celei mai mari întârzieri faţă de termenele impuse;

· minimizarea numărului de repere întârziate (faţă de termenele impuse);

· minimizarea sumei timpilor de pregătire - în cazul mai multor repere şi a unui singur utilaj;

Este clar că din combinarea factorilor mai sus amintiţi şi a criteriilor de performanţă adecvate rezultă o mare varietate de probleme de ordonanţare. Cercetările în domeniu - unele de ordin exclusiv "bibliografic" - au condus la identificarea a peste 3000 de probleme diferite.

Pentru uşurarea activităţii de inventariere şi clasificare a problemelor de ordonanţare a fost introdusă eticheta a / b / g în care:

· a este un câmp ce conţine informaţii privind numărul şi caracteristicile utilajelor precum şi ordinea de parcurgere a acestora;

· b este un câmp ce coţine informaţii privitoare la operaţii: termene impuse, termene de livrare,termene de eliberare ale utilajelor, precedenţele dintre operaţii (dacă există), posibilitatea de a intrerupe operaţiile etc;

· g este un câmp care specifică criteriul de performanţă utilizat;

In marea lor ,majoritate, problemele de ordonanţare sunt dificile în sensul că soluţia optimă este foarte greu de găsit dacă nu chiar imposibil de găsit în timp rezonabil chiar şi pentru probleme de gabarit "moderat". Acesta este şi motivul (a câta oară?) pentru care în asemenea situaţii se încearcă o rezolvare "aproximativă" bazată pe metode euristice.

5.2 Ordonanţarea pe o maşină

Un număr de repere (joburi) codificate 1,2,...,n trebuiesc lansate în execuţie pe un singur utilaj.

1) Fiecărui reper îi sunt asociate următoarele date:

· durata p_j;

· termenul impus d_j;

· termenul minim de lansare în execuţie r_j;

· termenul de livrare ;

· timpul de pregătire p_ij al utilajului pentru trecerea de la jobul i la jobul j;

Este clar că r_j + p_j £ d_j £ . Unele dintre aceste date pot fi ignorate într-un caz concret sau altul; în orice caz "obligatorii" sunt duratele şi în cele mai multe cazuri termenele impuse.

2) In ansamblul lor joburile pot fi:

· independente, putând fi lansate în fabricaţie în orice ordine;

· intercondiţionate;

3) Joburile pot fi executate:

· cu întrerupere;

· fără întrerupere;

4) Fiecărui job i se ataşează o variabilă C_j reprezentând momentul terminării execuţiei sale.

Notă: toate termenele impuse, de livrare, de terminare sunt raportate la un acelaşi moment de referinţă 0 astfel că toate sunt exprimate prin numere reale nenegative.

5) Calitatea unui program de lansare în execuţie a joburilor poate fi evaluată prin mai multe criterii de performanţă.

a) de tip loc îngust:

· minimizarea întârzierii maxime:

· minimizarea costului maxim datorat întârzierilor:

unde f_j(C_j) este o funcţie nedescrescătoare în variabilă C_j cu f_j(C_j) = 0 dacă C_j £ d_j;

b) de tip aditiv:

· minimizarea sumei costurilor datorate întârzierilor: ;

· minimizarea sumei ponderate a termenelor de terminare: ;

· minimizarea sumei întârzierilor efective: ;

· minimizarea numărului de joburi întârziate: unde

;

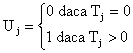c) care depind nu numai de caracteristicile individuale ale joburilor dar şi de ordinea în care sunt lansate în execuţie: ;

6) Codificarea a / b / g va avea, pentru problemele de ordonanţare pe o maşină, următoarea alcătuire:

· a = 1;

· indicatorul b va avea trei câmpuri b º ( ¾ , ¾ , ¾ ). In primul câmp se trec datele opţionale r_j,d_j,,p_ij luate în considerare. In al doilea câmp se specifică existenţa intercondiţionărilor prin simbolul p. In ultimul câmp se indică posibilitatea întreruperii execuţiei unui job prin simbolul P.

· indicatorul g specifică funcţia de optimizat.

7) Se observă uşor că prin combinarea tuturor elementelor amintite mai sus se obţine o mare varietate de situaţii de ordonanţare pe o maşină. Problemele asociate acestor situaţii se împart în:

· probleme uşoare: probleme pentru care se cunosc metode exacte de rezolvare ce determină soluţia optimă în timp polinomial;

· probleme grele: probleme pentru care metodele exacte de rezolvare cunoscute nu sunt polinomiale. Pentru rezolvarea aproximativă a acestor probleme se utilizează diferite euristici.

· probleme nedecise.

Câteva probleme de ordonanţare "uşoare" ,împreună cu metodele adecvate de rezolvare, vor fi prezentate în continuare.

1) 1 / d_j / L_max In această problemă se cunosc termenele impuse şi se cere ordonarea reperelor astfel încât să se minimizeze întârzierea maximă.

Soluţia optimă se obţine aplicând regula : are prioritate jobul cu termenul impus cel mai mic.

Exemplul 5.2.1 Pentru situaţia cu datele:

Reper	1	2	3	4	5	6	7
Durata p_j	3	4	4	6	9	11	15
Termene impuse d_j	22	28	36	21	15	35	31

Tabelul 5.1

durata de execuţie a tuturor reperelor este 3 + 4 + 4 + 4 + 6 + 9 + 11 + 12 = 52 unităţi de timp indiferent de ordinea în care sunt lansate în prelucrare; ordinea în care se minimizează întârzierea maximă este 5 ® 4 ® 1 ® 2 ® 7 ® 6 ® 3.

Reper j	5	4	1	2	7	6	3
Moment de terminare C_j	9	15	18	22	37	48	52
Intârziere faţă de termenul impus	-	-	-	-	6	13	16 = L_max

Tabelul 5.2

2) 1 / d_j , p / L_max Noua problemă diferă de precedenta prin existenţa unor relaţii de precedenţă între unele operaţii. Ea se rezolvă foarte simplu prin regula: dintre reperele încă neprogramate şi fără succesori direcţi se programează "cel mai târziu" reperul cu cel mai mare termen impus.

3) 1 / - / S w_jC_j In această situaţie, se urmăreşte minimizarea sumei ponderate a termenelor de terminare. Reperele vor fi lansate în ordinea în care rapoartele p_j/w_j formează un şir nedescrescător.

Exemplul 5.2.2

Reper j	1	2	3	4
Durata p_j	15	28	6	10		programul
Ponderea w_j	3	7	1	5	Þ	optim de	4 ® 2 ® 1 ® 3
p_j/w_j	5	4	6	2		lansare

Tabelul 5.3

4) 1 / / Faţă de prima problemă, acum se dau termene de livrare care, spre deosebire de termenele impuse, trebuiesc respectate. In plus, se urmăreşte minimizarea sumei termenelor de terminare ale operaţiilor. Următorul algoritm rezolvă problema indicând, dacă este cazul, incompatibilitatea ei.

Vom nota cu S mulţimea reperelor neprogramate.

Start S = {1,2,...,n}

Pasul 1. Se determină mulţimea: C = {k Î S ç} Dacă C este vidă Stop. Altminteri:

Pasul 2. Se selectează reperul k* Î C cu cea mai mare durată: şi se programează cel mai târziu.

Pasul 3. Se face actualizarea S = S \ {k*} şi se revine la pasul 1.

Deoarece la fiecare iteraţie se programează un reper, algoritmul se opreşte după n - 1 iteraţii.

Exemplul 5.2.3 In tabelul 5.4 se dau următoarele date privitoare la opt repere.

Reper	1	2	3	4	5	6	7	8
Durata	10	7	4	8	5	2	9	5
Termene de livrare	35	50	61	59	15	55	19	28

Tabelul 5.4

(aşa cum s-a mai spus, termenele de livrare sunt raportate la momentul de referinţă 0)

Start S = {1,2,3,4,5,6,7,8}

Iteraţia 1.

Pasul 1. =50 Þ C = {2,3,4,6};

Pasul 2. = 8 = p₄ Þ se programează la sfârşit reperul 4;

Pasul 3. S = {1,2,3,5,6,7,8}.

Iteraţia 2.

Pasul 1. =50 - 8 = 42 Þ C = {2,3,6};

Pasul 2. = 7 = p₂ Þ se programează la sfârşit reperul 2;

Pasul 3. S = {1,3,5,6,7,8}.

Iteraţia 3.

Pasul 1. =42 - 7 = 35 Þ C = {1,3,6};

Pasul 2. = 10 = p₁ Þ se programează la sfârşit reperul 1;

Pasul 3. S = {3,5,6,7,8}.

ş.a.m.d. După şapte iteraţii se obţin rezultatele sintetizate în următorul tabel:

Reper j	6	5	7	3	8	1	2	4
Durata p_j	2	5	9	4	5	10	7	8
Termen de începere	0	2	7	16	20	25	35	42
Termen de terminare C_j	2	7	16	20	25	35	42	50
Termen de livrare	55	15	19	61	28	35	50	59
S C_j	2	9	25	45	70	105	147	197

Tabelul 5.5

4)Alte exemple de probleme "uşoare" sunt 1 / d_j / S U_j în care se minimizează suma joburilor întârziate sau 1 / d_j / S w_jC_j în care se minimizează suma ponderată a termenelor de terminare.

Problema 1 / r_j , d_j / L_max este recunoscută a fi o problemă "dificilă". Dacă se compară noua situaţie cu cea din problema "uşoară" 1 / d_j / L_max se constată că "dificultatea" rezolvării se datorează prezenţei termenelor de disponibilitate r_j. Aici este interesant de menţionat faptul că dacă este permisă întreruperea operaţiilor, problemele 1 / r_j , d_j,P / L_max sau f_max şi chiar 1 / r_j , d_j, p, P / L_max sau f_max sunt "uşoare".

Deasemenea dificilă este şi problema 1 / d_j / S T_j în care se minimizează suma întârzierilor efective.

Despre problema 1 / r_j, p,`d_j, P / S C_j nu se poate spune, în prezent, dacă este uşoară sau dificilă.

5.3 Ordonanţarea în flux pe două maşini

Ordonanţarea în flux (Flow shop) este o problemă grea cu foarte puţine excepţii. Una dintre aceste excepţii este ordonanţarea pe două maşini. Problema este următoarea:

Un număr de repere 1,2,...,n sunt prelucrate fiecare întâi pe utilajul U₁ şi apoi pe utilajul U₂. Se cunosc duratele operaţiilor pe fiecare din cele două utilaje. Se cere determinarea ordinii de lansare în execuţie astfel încât durata realizării tuturor reperelor să fie minimă.

Pentru rezolvarea problemei se utilizează următorul algoritm, datorat lui Johnston.

Pasul 1. Se determină minimul duratelor tuturor operaţiilor.

· dacă acest minim reprezintă durate unei operaţii efectuate pe utilajul U₁ atunci reperul corespunzător se programează la început, bineînţeles după reperele anterior programate "la început";

· dacă minimul reprezintă durata unei operaţii efectuate pe utilajul U₂ reperul corespunzător se programează la sfârşit, dar înaintea celor deja programate "la sfârşit";

Pasul 2. Se elimină din listă reperul programat şi se reia pasul 1.

Observaţie In cazul în care minimul calculat în pasul 1 nu este unic, putem avea trei situaţii:

· minimul este egal cu durata unei operaţii pe primul utilaj dar şi cu durata unei operaţii pe al doilea utilaj. Reperul corespunzător operaţiei de pe primul utilaj se programează la început iar reperul corespunzător celeilalte operaţii, la sfârşit.

· minimul este egal cu duratele a două operaţii de pe primul utilaj. Se va plasa mai în faţă reperul a cărui operaţie pe al doilea utilaj durează mai puţin.

· minimul este egal cu duratele a două operaţii pe al doilea utilaj. Se va plasa mai la sfârşit reperul a cărui operaţie pe primul utilaj durează mai puţin.

Exemplul 5.2.4 Aplicând algoritmul descris problemei cu datele din tabelul 5.6

Reper j

Durata operaţiei pe utilajul U₁

Durata operaţiei pe utilajul U₂

Tabelul 5.6

se obţine următorul program optim de lansare: 3 ® 1 ® 5 ® 6 ® 2 ® 4. Programarea în timp a execuţiei rezultă din diagrama:

Utilaj U₁

R₃

R₁

R₅

R₆

R₂

R₄

Utilaj U₂

R₃

R₁

R₅

R₆

R₂

R₄

Termenele de începere ale diferitelor operaţii

Figura 5.1

Timpul total de prelucrare al tuturor reperelor este de 35 de unităţi de timp.

Problema generală de ordonanţare Job shop este de departe cea mai complicată. Un număr de repere 1,2,...,m se prelucrează pe n utilaje 1,2,...,n fiecare reper parcurgând utilajele într-o anumită ordine dictată de tehnologia de fabricaţie. Se presupun cunoscute duratele operaţiilor. Reamintim că un utilaj nu poate procesa la un moment dat decât un singur reper. Nu există restricţii privind ordinea în care se execută operaţiile de prelucrare ale diferitelor repere pe un acelaşi utilaj. Cum trebuiesc lansate reperele pentru ca timpul total de prelucrare să fie minim?

Spaţiul limitat nu ne îngăduie să zăbovim asupra acestei probleme care – ea singură – poate constitui subiectul unei cărţi de sine stătătoare!

§ 6. Problema stabilirii traseelor de transport

Într-o formă simplificată, problema stabilirii traseelor de transport ( pe scurt problema STT) se enunţă astfel:

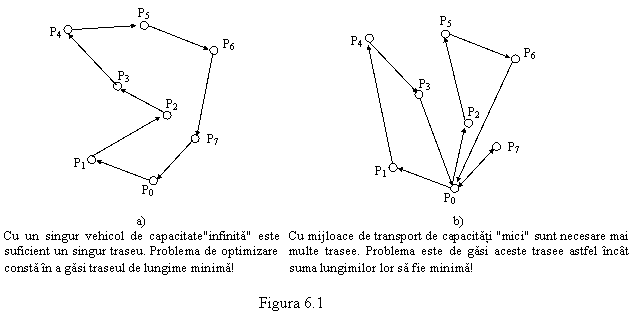
O firmă urmează să livreze un produs mai multor clienţi P₁ , P₂ ,..., P_n în cantităţile q₁ , q₂ ,...,q_n. Livrările se fac de la un depozit al firmei, notat P₀ , folosindu-se pentru aceasta un parc de mijloace de transport de diferite capacităţi.Fie T₁ ,T₂ ,...,T_m tipurile acestor vehicule diferenţiate atât prin capacităţile lor c₁ , c₂ ,..., c_m cât şi prin numărul s₁ , s₂ ,..., s_m de unităţi disponibile pentru efectuarea transporturilor.Prin contract, cererea fiecărui client trebuie onorată la un singur transport. Fiecare vehicol inclus în programul de livrări pleacă de la depozitul P₀ încărcat sau nu la capacitatea maximă, vizitează succesiv un număr de clienţi şi după ce se goleşte se întoarce la depozit pentru o eventuală nouă încărcare şi trimitere pe teren. În acest context, se pune problema de a stabili traseele de vizitare ale clienţilor precum şi tipul si numărul de mijloace de transport necesare satisfacerii tuturor cererilor astfel încât distanţa totală parcursă să fie minimă.

Problema STT este una din cele mai complexe probleme de optimizare combinatorială. Ea este o generalizare a problemei comisvoiajorului; Intr-adevăr, dacă ar exista un singur mijloc de transport a cărui capacitate acoperă suma tuturor cererilor clienţilor atunci STT se reduce la determinarea ordinii în care clienţii sunt vizitaţi astfel încât distanţa totală parcursă să fie minimă (vezi fig. 6.1)

Au fost propuse un număr de metode exacte de rezolvare a problemei STT dar eficacitatea lor - pe probleme reale, de dimensiuni mari - este destul de redusă. Mult mai atractive s-au dovedit metodele euristice, capabile să ofere în timp util şi cu un efort de calcul rezonabil soluţii acceptabile. Un exemplu de metodă de rezolvare aproximativă este procedura Clarke - Wright [ ], descrisă succint în continuare.

1) La început se consideră că fiecare client este aprovizionat direct de la depozit cu un mijloc de transport special detaşat să facă acest lucru. (vezi fig. 6.2)

2) În continuare se încearcă concatenarea acestor trasee în scopul reducerii distanţei totale. Să examinăm fig 6.3a):

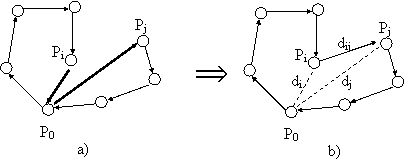
Figura 6.3

în care apar două trasee de lungimiD , D'. În fiecare traseu s-au pus în evidenţă doi clienţi P_{i ,}P_j vecini cu depozitul P₀ (relativ la un traseu dat un client se va numi vecin cu P₀ dacă el este fie primul fie ultimul client vizitat; doi clienţi se vor zice vecini dacă în traseul dat ei sunt vizitaţi consecutiv) Concatenarea este ilustrată în fig. 5.3b). Din figură se vede că lungimea traseului rezultat este egală cu:

(D - d_i) + d_ij + (D' - d_j) = D + D' - (d_i + d_j - d_ij) = D + D' - s_ij (6.1)

unde:

s_ij = d_i + d_j - d_ij

d_ij fiind distanţa dintre P_i şi P_j. Mărimile s_ij , 1 £ i ¹ j £ n se numesc generic reduceri. Este evident că:

s_ij ³ 0 şi s_ij = s_ji

Din (6.1) rezultă atunci că, prin concatenarea a două trasee distanţa totală parcursă se micşorează.

3) Revenind la fig 6.3a) fie Q şi Q' totalurile cererilor clienţilor de pe cele două trasee. Cum fiecare traseu este deservit de un singur mijloc de transport este clar că pe cele două trasee sunt fixate două vehicole ale căror capacităţi de transport - eventual diferite - acoperă cantităţile Q şi Q'. Pe traseul din fig. 6.3b) va trebui transportată cantitatea Q + Q' şi aceasta de către un singur vehicol! În concluzie concatenarea celor două trasee este admisibilă numai dacă se dispune de un mijloc de transport a cărui capacitate acoperă sumă Q + Q'.

4) Deoarece la un moment dat pot exista mai multe concatenări admisibile, are prioritate aceea care produce cea mai mare reducere a distanţei totale de parcurs.

5) Procesul se opreşte în momentul în care nu mai există concatenări admisibile.

Exemplu 6.1 Se consideră reţeaua din fig. 6.4. Cantităţile comandate q_i , distanţele d_i de la depozitul P₀ la clienţii P_i distanţele d_ij dintre clienţi şi reducerile s_ij = d_i + d_j - d_ij sunt indicate în tabelul 6.1. Firma are disponibile numai vehicole cu capacitatea de 6000 unităţi.

Client

P_i

Cerere

q_i

Distanţa

d_i:P₀- P_i

Trasee

Cant. circulată

pe un traseu

P₁

P₂

P₃

P₄

P₅

P₆

P₇

P₁

1100

316

1100

316

224

247

608

640

539

632

849

P₂

1300

224

1300

363

400

212

424

400

500

167

640

P₃

1200

539

1200

635

316

197

566

215

640

622

500

P₄

1200

412

1200

320

316

367

361

771

224

P₅

1900

224

1900

440

100

395

412

P₆

1800

316

1800

499

400

P₇

1700

583

1700

Tabelul 6.1

La start se presupune că fiecare client P_i este servit de un singur mijloc de transport care face traseul P₀ ® P_i® P₀ ; vor fi deci şapte trasee însumând 2(d₁ + d₂ + ... +d₇) = 5228 km şi implicând şapte vehicule ( a căror capacitate este folosită parţial...)

Iteraţia 1 Cea mai mare reducere este s₄₇ = 771. Concatenăm traseele P₀ ® P₄® P₀ şi P₀ ® P₇® P₀ în traseul P₀ ® P₄ ® P₇ ®P₀ obţinând o reducere a distanţei totale de 771 km. Pe acest traseu va circula un singur mijloc de transport cu încărcătura iniţială de 1200 + 1700 = 2900 u. Rămân şase trasee însumând 5228 - 771 = 4457 km. Vezi tabelul 6.2

Iteraţia 2 Cea mai mare reducere admisibilă - pusă în evidenţă şi în tabelul6.2 - este s₃₄ = 635. Concatenăm traseele P₀ ® P₃® P₀ şi P₀ ® P₄ ® P₇ ®P₀ în traseul P₀ ® P₃ ® P₄ ®P₇ ®P₀ pe care se va transporta 2900 + 1200 = 4100 u. Numărul de trasee (şi implicit de vehicule folosite) s-a redus la cinci însumând 4457 - 635 = 3822 km. Rezultă situaţia din tabelul 6.3

	Cant. circulată pe un traseu	Clienţi	Trasee	P₁	P₂	P₃	P₄	P₅	P₆	P₇
	1100	1	(1)® ¬
	1300	2	(2)® ¬
	1200	3	(3)® ¬				635
	2900	4	(4)®							771
	1900	5	(5)® ¬
	1800	6	(6)® ¬
-		7	¬

Tabelul 6.2

Cant. circulată pe un traseu	Clienţi	Trasee	P₁	P₂	P₃	P₄	P₅	P₆	P₇
1100	1	(1)® ¬
1300	2	(2)® ¬
4100	3	(3)®				635
-	4								771
1900	5	(4)® ¬
1800	6	(5)® ¬							499
-	7	¬

Tabelul 6.3

Iteraţia 3 Următoarea reducere (ca mărime) este s₃₇ = 622 ea se exclude deoarece P₃ şi P₇ sunt deja pe acelaşi traseu. Reducerea care va fi luată în considerare este s₆₇ = 499 (indicată şi în tabelul 6.3) Se vor concatena traseele P₀ ® P₃® P₀ şi P₀ ® P₃ ® P₄ ®P₇ ®P₀ în traseul P₀ ® P₃ ® P₄ ®P₇ ®P₆ ®P₀ dealungul căruia se va livra cantitatea 4100 + 1800 = 5900 u. (< 6000 u. º capacitatea unui vehicul) Au rămas patru trasee însumând 3822 - 499 = 3323 km şi se utilizează patru mijloace de transport, unul fiind încărcat aproape la capacitatea maximă. Vezi tabelul 6.4

Iteraţia 4 Cea mai mare reducere admisibilă este acum s₁₂ = 316. Se vor concatena traseele P₀ ® P₁® P₀ şi P₀ ® P₂® P₀ într-unul singur pe care se va transporta cantitatea 1100 + 1300 = 2400 u. Acum sunt numai trei trasee şi trei vehicule iar distanţa totală s-a redus la 3323 - 316 = 3007 km. Noua situaţie este rezumată în tabelul 6.5

Iteraţia 5 Următoarea reducere admisibilă este s₂₅ = 48. Concatenăm traseele P₀ ® P₁® P₂ ® P₀ şi P₀ ® P₅® P₀ în traseul P₀ ® P₁® P₂ ® P₅® P₀ pe care se va livra cantitatea 2400 + 1900 = 4300 u. Au rămas două trasee fiecare deservit de un vehicul. Distanţa totală de parcurs va fi: 3007 - 48 = 2959 km. Este clar că cele două trasee numai pot fi concatenate din cauza capacităţii limitate de transport a vehiculelor. Vezi tabelul 6.6 Cele două trasee sunt vizualizate în fig.6.5

Cant. circulată pe un traseu	Clienţi	Trasee	P₁	P₂	P₃	P₄	P₅	P₆	P₇
1100	1	(1)® ¬		316
1300	2	(2)® ¬
5900	3	(3)®				635
-	4								771
1900	5	(4)® ¬
-	6	¬							499
-	7

Tabelul 6.4

Cant. circulată pe un traseu	Clienţi	Trasee	P₁	P₂	P₃	P₄	P₅	P₆	P₇
2400	1	(1)®		316
-	2	¬					48
5900	3	(3)®				635
-	4								771
1900	5	(4)® ¬
-	6	¬							499
-	7

Tabelul 6.5

Cant. circulată pe un traseu	Clienţi	Trasee	P₁	P₂	P₃	P₄	P₅	P₆	P₇
4300	1	(1)®		316
-	2						48
5900	3	(3)®				635
-	4								771
	5	¬
-	6	¬							499
-	7

Tabelul 6.6

§ 7. Întrebări şi probleme

1.Ce este o problemă combinatorială? Dar o problemă de optimizare combinatorială? Daţi un exemplu diferit de cele oferite în carte şi discutaţi-l cu colegii şi cu profesorul dvs.

2.Ce înseamnă că o problemă de optimizare este uşoră (grea)? Daţi exemple din fiecare categorie.

3.Rezolvaţi problema din exemplul 3.2.

Text Box: ¥ 10 7 9 11
8 ¥ 11 12 4
9 11 ¥ 13 6
6 12 14 ¥ 7
10 5 8 8 ¥

Tabelul 7.1

4. Un comisvoiajor situat în localitatea 0 are de vizitat oraşele 1,2,3,4. Costurile de deplasare dintr-un oraş în altul sunt date în tabelul 7.1 (Se observă că în general c_ij ¹ c_ji, altfel spus costul deplasării între două localităţi depinde de sensul de deplasare - avem de a face cu o problemă asimetrică !)

Să se aplice algoritmul de tip Branch & Bound al lui Eastman

pentru a gă si un traseu de cost minim.

5. Într-o regiune a ţării se afla şapte puncte de interes turistic. Poziţiile relative ale celor şapte puncte sunt date în fig. 7.1.iar distanţele dintre ele sunt date în tabelul alăturat 7.2.

O agenţie de turism este interesată în determinarea celui mai scurt traseu de vizitare a celor şapte obiective.

Rezolvaţi problema utilizând euristica E₃ şi ajustarea locală E₂.

6.Un comisvoiajor pleacă din localitatea 0 şi trebuie să viziteze localităţile 1,2,...,6 (fiecare o singură dată) la sfârşitul călătoriei urmând a se reîntoarce în punctul de plecare 0 (vezi fig.7.2) În tabelul alăturat 7.3 se dau distanţele între localităţi.

a) Să se determine un traseu complet folosind euristica E₁: "mergi la cel mai apropiat vecin".

b) Eliminaţi eventualele încrucişări folosind euristica E₂ de ajustare locală. Ce lungime va avea noul traseu?

c) Determinaţi un arbore de lungime minimă care să conecteze cele şapte localităţi după care aplicaţi euristica E₃ pentru a obţine un traseu complet.

d)Reluaţi punctul c) folosind de această dată euristica E₄.

7.Firma X produce pâine pe care o desface către populaţie prin 12 magazine de specialitate. Fabrica de pâine şi centrele de desfacere sunt localizate în punctele P₀ , P₁ ,..., P₁₂ indicate în figura 7.3. Pentru ziua următoare cererile sunt date întabelul 7.4:

	Centre P_i	P₁	P₂	P₃	P₄	P₅	P₆	P₇	P₈	P₉	P₁₀	P₁₁	P₁₂	Total
	Cerere (buc.) q_i	2200	300	800	1100	900	700	1400	1600	1600	1800	500	1500	14400

Tabelul 7.4

Transportul se face cu vehicule cu capacitatea de 4500 buc.

Distanţele d_i de la fabrica P₀ la centrele P_i ca şi distanţele d_ij dintre centre de desfacere se vor calcula cu relaţia lui Pitagora ţinând cont de faptul că unitatea de măsură a grilei din fig. 7.3 este de 200m. De exemplu distanţa dintre P₁ şi P₇ va fi:

a) Să se determine traseele de transport. cantităţile transportate, lungimile traseelor şi distanţa totală de parcurs.

b)Care va fi soluţia problemei în cazul în care firma are două vehicole cu capacitatea de 4500 buc. şi alte patru cu capacitatea de 2000 buc.?

8. Explicaţi termenii flow shop, open shop, job shop din problema ordonanţării.

9. Se pune problema lansării în execuţie a opt repere 1,2,...,8 pentru care se cunosc:

· duratele p₁ , p₂ ,..., p₈;

· termenele de livrare .(vezi tabelul 7.5 )

În ce ordine trebuie lansate în execuţie reperele astfel încât:

· termenele de livrare să nu fie depăşite:

· suma termenelor de terminare să fie minimă:

Cod reper: j	1	2	3	4	5	6	7	8
Durata : p_j	10	19	14	8	23	17	9	5
Termen de livrare: d_j	25	45	90	100	80	105	50	20

Tabelul 7.5

4. Zece repere se prelucrează în flux pe două utilaje: prima operaţie se execută pe utilajul A iar a doua pe utilajul B. În tabelul 7.6 se dau duratele de excuţie ale celor două operaţii pentru fiecare reper în parte. În ce ordine vor fi lansate cele zece repere astfel încât durata totală de execuţie să fie minimă?

Repere

Utilaje

Tabelul 7.6

b) Aceeaşi chestiune cu datele:

Repere	1	2	3	4	5	6	7
A	11	6	8	15	9	14	13
B	8	11	8	10	12	6	9

Tabelul7.7