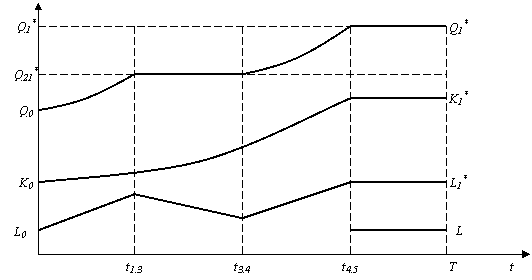
Model Dinamic de Analiză a Activităţii

Fără Împrumuturi şi Granturi

Ipoteza 1: Firma produce un bun omogen folosind doi factori de producţie: capitalul şi munca.

Ipoteza 2: Modelul dinamic de analiză este un model cu factori de producţie complementari, funcţia de producţie este liniară, proporţia între factorii de producţie rămânând constantă. Activitatea de producţie este un proces prin care este fabricat produsul finit din muncă şi capital. Sunt presupuse două activităţi de producţie:

- activitatea 1: capital intensivă (raportul K/L este mare);

- activitatea 2: forţa de muncă intensivă (raportul K/L este mic).

Funcţia de producţie este dată de:

(1) Q(t) = q₁K₁(t) +q₂K₂(t)

unde Q(t) este producţia fizică (omogenă).

Veniturile sunt constante la scala de fabricaţie (funcţia de producţie este liniară).

Productivitatea medie a capitalului din activitatea j = 1,2 este:

q_j = , j = 1,2

Ecuaţia de formare a forţei de muncă este:

(2) L(t) = l₁K₁(t) + l₂K₂(t)

iar compoziţia organică a capitalului:

l_j = , j =1,2

Ecuaţia de formare a bunurilor capital:

(3) K(t) = K₁(t) + K₂(t)

Ipoteza 3: Pentru activitatea 1 – activitate capital intensivă, vom avea condiţiile:

K₁ > K₂

L₁ < L₂

de unde rezultă:

productivitatea muncii este mai mare în activitatea 1.

Ipoteza 3’: Piaţa producţiei finite este cu competiţie imperfectă:

Ipoteza 4: Funcţia de câştig:

(4) S(K₁(t), K₂(t)) = (q₁p(Q)-wl₁) + (q₂p(Q)-wl₂)K₂(t)

Ipoteza 5: Singura structură de finanţare este autofinanţarea:

(5) X(t) = K(t)

Ipoteza 6: Ecuaţia de evoluţie a acţiunilor:

(6) = S(K₁(t), K₂(t)) – aK(t) – D(t); X(0) = K₀ > 0

Ipoteza 7: Ecuaţia de evoluţie a bunurilor capital (investiţia netă):

(7) = I(t) – aK(t); K(0) = K₀ > 0

Ipoteza 8: Funcţionala obiectiv:

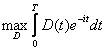+ X(T)e^-iT

Restricţii momentane:

(8) D(t) 0

(9) K₁(t)0

(10) K₂(t)0

Din I(t) – aK(t) = S(K₁, K₂) – aK(t) – D(t)

(11) D(t) = S(K₁, K₂) – I(t)0

înlocuim X(t) cu K(t) şi K₂(t) cu K(t) – K₁(t) şi vom obţine modelul:

(12) 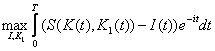+ K(T)e^-iT

(13) = I(t) – aK(t); K(0) = K₀ > 0

(14) K(t) – K₁(t)0

(15) K₁(t)0

(16) S(K₁(t), K₂(t)) – I(t)0

Rezolvarea modelului

Lagrangeanul problemei:

(17) L(K(t),I(t),K₁(t),l(t),m₁(t),m₂(t),m₃(t)) = (S(K(t), K₁(t)) – I(t))(1+m₃(t)) + l(t)(I(t) – aK(t)) + m₁(t)(K(t) – K₁(t)) + m₂(t)K₁(t)

Condiţiile de optim:

(18)

(19)

(20)

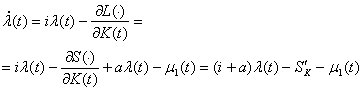
(21) m₁(t)(K(t) – K₁(t)) = 0

(22) m₂(t)K₁(t) = 0

(23) m₃(t) (S(K(t), K₁(t)) – I(t)) = 0

(24) m₁(t), m₂(t), m₃(t)0

(25) l(T) = 1

Datorită concavităţii Lagrangeanului şi a restricţiilor, condiţiile necesare sunt şi suficiente.

Calcule preliminare:

(26) Q(t) = (q₁ – q₂)K₁(t) + q₂K(t); L(t) = (l₁ – l₂)K₁ + l₂K(t)

(27) S(K(t), K₁(t)) = V(Q) – (wl₁ – wl₂)K₁(t) – wl₂K(t); V(Q) = p(Q)Q

(28) ;

(29)

(30)

Observaţie:

;

Costurile unitare:

(31) c_j = , c₁ c₂ c₂₁

unde:

wl_j – salariile pe o unitate de bun capital

i – revenirea pe o unitate de capital investit (de bun capital)

a – amortizarea pe o unitate de bun capital

(32) c₂₁ =

c₂₁ – costul unitar al trecerii de la activitatea 2 la activitatea 1

Traiectorii admisibile

Tr. Nr.	m1(t)	m2(t)	m3(t)	Activitatea		Q	Politica firmei
1	0	+	+	2	+	<^Q*21	creştere cu activitatea 2
2	0	+	0	2	0	Q^*2	staţionară, dividende, activitatea 2
3	0	0	+	21	+	Q^*21	trecere de la activitatea 2 la activitatea 1
4	+	0	+	1	+	>Q^*21	creştere cu activitatea 1
5	+	0	0	1	0	Q^*1	staţionară, dividende, activitatea 1

Traiectorii inadmisibile

a) m₁(t) > 0, m₂(t) > 0 Þ K(t) = K₁(t), K(t) = 0 Þ K(t) = 0 exclus prin ipoteză.

b) m₁(t) = 0, m₂(t) = 0, m₁(t) > 0, m₃(t) = 0

din (19) Þ S’_K = 0 Þ 0 = V’_Q(q₁ – q₂) + w(l₂ – l₁) Þ

l(t) = m₃(t) + 1 Þ ;

dacă m₁(t) = m₃(t) = 0 Þ din (20) Þ 0 = (i + a)(1+ m₃(t)) – S’_K + m₁(t) Þ S’_K = i + a Þ q₂V’_Q = S’_K + wl₂ Þ V’_Q = (i + a + wl₂)= c₂

Contradicţie: venitul marginal din vânzări este simultan egal cu costul marginal al activităţii 21 şi al activităţii 2.

Ipoteză:

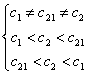sau , j = 1, 2, 21

Traiectoria 1: m₁ = 0, m₂ > 0, m₃ > 0

(18) Þ l(t) = 1 + m₃(t) Þ ,

(20) Þ = (i + a) (1+ m₃(t)) – S’_K

(21) Þ K(t) > K₁(t)

(22) Þ K₁(t) = 0; deci K(t) = K₁(t) > 0

(23) Þ S(K(t), K₁(t)) – I(t) = 0 Þ D(t) = 0; deci nu se plătesc dividende, tot ceea ce se câştigă se reinvesteşte.

S(K₁(t),K₂(t)) = I(t) Þ Þ (ecuaţia de balanţă fiind K(t) = X(t))

(19)Þ

(29)ÞÞ

Pe traiectoria 1, .

- la începutul traiectoriei:

- la sfârşitul traiectoriei:

La sfârşitul traiectoriei 1:

Traiectoria 2: m₁(t) = 0, m₂(t) > 0, m₃(t) = 0

(18) Þ l(t) = 1

(19) Þ

(19)+(29)Þ

(20) Þ 0 = (i + a) – S’_K Þ S’_K = (i + a)

(30)Þ, traiectoria 2 este staţionară.

(23) Þ , se plătesc dividende.

(22) Þ K(t) = 0 Þ K(t) = K₂(t)

(21) Þ K(t) > K₁(t) > 0; rezultă Q^*₂ < Q^*₂₁ Þ c₂₁ < c₂ < c₁.

Traiectoria 3: m₁(t) = 0, m₂(t) = 0, m₃(t) > 0

(18) Þ l(t) = m₃(t) + 1

(19) Þ Þ

(20) Þ

(21) Þ K(t) = K₁(t) Þ K₂(t) = 0

(22) Þ K₁(t) > 0; deci rezulta ca si (este activitate de relocare)

(23) Þ

Pe traiectoria 3: m₃(t) > 0

- la începutul traiectoriei: ,

Þ (i + a)(1 + m₃(t)) – S’_K > 0 Þ S’_K < (i + a)(1 + m₃(t)) Þ (deoarece m₃(t) = 0) Þ S’_K < (i + a) Þ Þ Q(t) > Q^*₂ Þ Q^*₂₁ > Q^*₂ Þ c₁ < c₂ < c₂₁

Traiectoria 4: m₁(t) > 0, m₂(t) = 0, m₃(t) > 0

(18) Þ l(t) = m₃(t) + 1

(19)Þ Þ

(20) Þ

(21) Þ K(t) = K₁(t) Þ K₂(t) = 0

Q(t) = (q₁-q₂)K₁(t) + q₂K(t) = (q₁ – q₂) K₁(t) + q₂K₁(t) = q₁K₁(t)

= V – (wl₁ – wl₂)K₁(t) – wl₂K(t) = V – (wl₁ – wl₂)K₁(t) – wl₂K₁(t) = V – wl₁K₁(t)

Pe traiectoria 4: m₃(t) > 0

- la începutul traiectoriei: ,

Þ – S’_K > m₁(t) - (i + a)(1 + m₃(t)) Þ S’_K < - m₁(t) + (i + a)(1 + m₃(t)) Þ (deoarece m₃(t) > 0) Þ S’_K < (i + a)(1 + m₃(t)) Þ S’_K < (i + a) Þ Þ Q(t) > Q^*₁

- la sfârşitul traiectoriei 4: ,

Þ S’_K > i + a Þ Þ Q(t) < Q₁^*

Q₂₁^* < Q(t) < Q₁^* Þ c₁ < c₂ < c₂₁

Traiectoria 5: m₁(t) > 0, m₂(t) = 0, m₃(t) = 0

(18) Þ l(t) = 1 Þ

(19)Þ Þ Q(t) > Q₂₁^*

(20) Þ Þ - S’_K = m₁(t) – (i + a) Þ S’_K = i + a - m₁(t) Þ

(21) Þ K(t) = K₁(t) Þ K₂(t) = 0

(22) Þ K₁(t) > 0

(23) Þ S(t) – I(t) > 0 Þ S(t) > I(t) Þ D(t) > 0

Observaţie:

, deoarece

Þ Q(t) = Q₁^*, traiectorie staţionară.

Rezultă Q₁^* > Q₂₁^* Þ c₁ < c₂ < c₂₁

Traiectorii finale

Trebuie să verifice condiţiile de transversalitate:

l(T) = 1

l(T) = m₃(T) + 1 Þ m₃(T) = 0 Þ numai traiectoriile 2 şi 5 pot fi traiectorii finale.

Traiectoria 2 este finală dacă K(T) = K₂(T) si c₂₁ < c₂ < c₁.

Traiectoria 5 este finală dacă K(T) = K₁(T) si c₁ < c₂ < c₂₁.

REZUMAT

Tr. Nr.	m1(t)	m2(t)	m3(t)	Activitatea		Q	Politica firmei
1	0	+	+	2	+	<Q^*21	creştere cu activitatea 2
2	0	+	0	2	0	Q^*2	staţionară, dividende, activitatea 2
3	0	0	+	21	+	Q^*21	relocare de la activitatea 2 la activitatea 1
4	+	0	+	1	+	>Q^*21	creştere cu activitatea 1
5	+	0	0	1	0	Q^*1	staţionară, dividende, activitatea 1

Traiectorii de magistrală care se finalizează cu Traiectoria 2

TR1®TR2

TR1: Q(t) < Q₂^*; TR2: Q₂^*;® K(t) poate fi continuă şi poate creşte.

TR3®TR2

TR2: Q(t) = Q₂^*; TR2: Q(t) = Q₂₁^*; ®K(t) este discontinuă, TR3 nu poate fi predecesoare.

TR4®TR2

TR2: c₂₁ < c₂ < c₁; TR4: c₁ < c₂ < c₂₁; contradicţie.

TR5®TR2

TR5: K(t) = K₁^*; TR2: K(t)=K₂^*; ®discontinuitatea lui K(t).

Predecesoarele Traiectoriei 1

Traiectoria 2	NU	K discontinuă
Traiectoria 3	NU	K discontinuă
Traiectoria 4	NU	K discontinuă
Traiectoria 5	NU	TR1: c21 < c2 < c1; TR5: c1 < c2 < c21

Traiectorii de magistrală care se finalizează cu Traiectoria 5

Predecesoarele Traiectoriei 5

Traiectoria 1	NU	K discontinuă
Traiectoria 2	NU	inadvertenţă de costuri
Traiectoria 3	NU	K discontinuă
Traiectoria 4	DA

Predecesoarele Traiectoriei 4-5

Traiectoria 1	NU	K discontinuă
Traiectoria 2	NU	inadvertenţă de costuri
Traiectoria 3	DA
Traiectoria 4	NU	K discontinuă

Predecesoarele Traiectoriei 3-4-5

Traiectoria 1	DA
Traiectoria 2	NU	inadvertenţă de costuri
Traiectoria 3	NU	K discontinuă
Traiectoria 4	NU	K discontinuă

Predecesoarele Traiectoriei 1-3-4-5

Traiectoria 1	NU	K discontinuă inadvertenţă de costuri
Traiectoria 2	NU	K discontinuă
Traiectoria 3	NU	K discontinuă
Traiectoria 4	NU	K discontinuă

Dacă c₂₁ < c₂ < c₁ Þ magistrala TR1®TR2

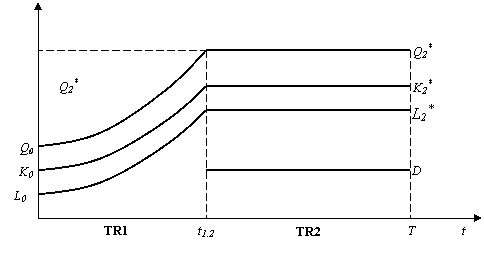
Dacă c₁ < c₂ < c₂₁ Þ magistrala TR1®TR3®TR4®TR5