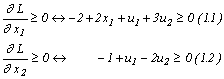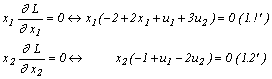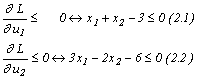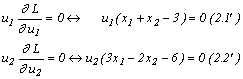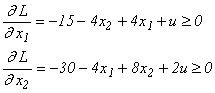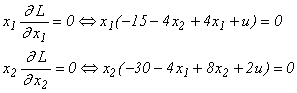CAPITOLUL IV

ELEMENTE DE PROGRAMARE NELINIARA

§ 1.Introducere

Caracteristic unei probleme de programare liniară este faptul că toate funcţiile implicate în ea – funcţia obiectiv şi restricţii – sunt liniare. Deşi ipotezele de liniaritate au loc în numeroase situaţii practice tot atât de frecvent ale nu sunt îndeplinite. De fapt, mulţi economişti teoreticieni au constatat că un anume grad de neliniaritate este regula şi nu excepţia în problemele de planificare economică.

Există deci o puternică motivaţie economică pentru studiul problemelor de programare neliniară a căror formă canonică de prezentare este:

Û

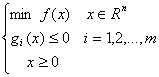
Dacă în cazul liniar (Û f si g_i sunt funcţii liniare) există (cel puţin) o metodă generală de rezolvare – de exemplu metoda simplex – în cazul neliniar nu există o asemenea metodă. Totuşi progrese substanţiale au fost făcute în unele cazuri speciale prin impunerea unor condiţii asupra funcţiilor f si g_i .Aria acestor cazuri speciale este destul de mare astfel că nu ne vom putea opri decât asupra unora mai relevante.

§ 2. Neliniaritatea în modelarea proceselor economice. Câteva exemple

Să considerăm problema firmei al cărei obiectiv este determinarea unui program de producţie astfel încât:

· necesarul de resurse pentru susţinerea programului să se încadreze în disponibile date;

· profitul total, rezultat din vânzarea bunurilor produse să fie maxim.

În multe situaţii practice, preţurile şi costurile unitare de fabricaţie pot fi considerate constante astfel că şi profiturile unitare vor fi la fel. În consecinţă, în aceste cazuri funcţia obiectiv, care reprezintă profitul total, va fi liniară:

(x_j reprezintă cantitatea produsă şi vândută din bunul j;P_j este profitul unitar corespunzător bunului j )

Nu întotdeauna tot ceeace se produce dintr-un bun se poate şi vinde la un anumit preţ. Apare aşa numita problemă a elasticităţii preţului: cantitatea de marfă vândută se află într-o relaţie inversă cu preţul cerut aşa cum arată curba preţ – cerere (fig. 2.1a)

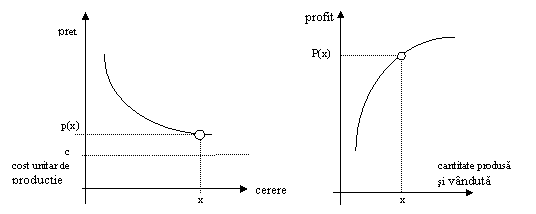
p(x) este preţul care permite firmei să vândă x unităţi de produs

a) b)

Figura 2.1

Dacă c este costul unitar de producţie, cost pe care îl presupunem – pentru simplificarea expunerii – fix, atunci profitul firmei, rezultat din producerea şi vânzarea cantităţii x este dat de funcţia neliniară (vezi fig. 2.1b):

P(x) = x.p(x) – c(x)

Dacă fiecare din produsele firmei are o asemenea funcţie profit, notată P_j(x_j), profitul total va fi exprimat prin funcţia neliniară:

O altă sursă de neliniarităţi în funcţia obiectiv o constituie variaţia costului marginal - pentru producerea a încă unei unităţi dintr-un produs - în funcţie de nivelul producţiei. Acest cost marginal poate să scadă în unele situaţii (ca urmare a trecerii la producţia de serie, al acumulării experienţei şi al perfecţionării procesului de producţie) iar în altele poate să crească (ore suplimentare,utilizarea în regim de urgenţă a unor capacităţi de producţie mai costisitoare pentru satisfacerea unor cereri imediate)

Neliniaritatea poate apare şi în restricţii într-o manieră asemănătoare. De exemplu, dacă există o restricţie bugetară asupra costului producţiei, relaţia corespunzătoare va fi cu siguranţă neliniară în cazul în care costul marginal al producţiei este variabil.

Pentru restricţiile privitoare la alte tipuri de resurse, neliniaritatea apare ori de câte ori consumurile nu sunt direct proporţionale cu nivelele de producţie.

Exemplul 2.1 În problema transporturilor se urmăreşte determinarea unui program pentru transportul unui produs de la diferite surse la diverşi consumatori, cunoscându-se cantităţile disponibile şi cererile, astfel încât costul total al transportului să fie minim. În programarea liniară, costul transportului unei unităţi de produs de la o anumită sursă la o anumită destinaţie a fost considerat constant, independent de cantitatea transportată. De multe ori se întâmplă ca la cantităţi mari să se acorde la transport anumite reduceri; în aceste situaţii, costul marginal al transportului unei unităţi suplimentare tinde să scadă şi ca o consecinţă costul C(x) al transportării cantităţii x este dat de o funcţie neliniară. Să analizăm datele din fig. 2.2 a) şi b).

cost marginal cost

a) b)

Figura 2.2

Fie x cantitatea transportată şi C(x) costul transportării cantităţii x.

· dacă 0 £ x £ 6 costul unitar de transport este de 6.5 u.m. deci

C₁(x) = 6.5x u.m.;

· dacă 6 £ x £ 15 , 6 unităţi vor fi transportate cu costul 6.5 u.m. per unitate iar următoarele cu numai 5 u.m. per unitate astfel că :

C₂(x) = 6.5 ´6 + 5.(x - 6) = 9 + 5.x

· dacă 15 £ x £ 27 , 15 unităţi vor fi transportate cu costul C₂(15) = 84 iar următoarele cu numai 4 u.m. per unitate. Costul total va fi :

C₃(x) = 84 + 4.(x – 15) = 24 + 4.x

· dacă 27 < x £ 45 , 27 unităţi vor fi transportate cu costul C₃(27) = 132 iar următoarele cu 3 u.m. per unitate de unde costul total:

C₄(x) = 132 + 3.(x – 27) = 51 + 3.x

Prin urmare, costul C(x) al transportării a x unităţi este dat de funcţia:

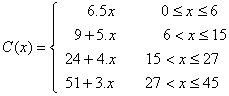
care este neliniară dar “liniară pe porţiuni”. Din fig. 4.2b) rezultă că pantele porţiunilor liniare ale graficului funcţiei C(x) sunt chiar costurile marginale evidenţiate în fig 4.2a).

Dacă fiecare cuplu (sursă i , destinaţie j ) are o funcţie cost similară, aşa încât costul transportului a x_ij unităţi de la i la j este dat de funcţia neliniară C_ij(x_ij) atunci costul total este reprezentat de funcţia de asemenea neliniară;

Aceste consideraţii nu modifică restricţiile problemei de transport care rămân liniare:

suma cantităţilor livrate de sursa i nu depăşeşte disponibilul său;

suma cantităţilor primite de consumatorul j acoperă cererea sa.

Exemplul 2.2 La terminalul unei conducte petroliere situat într-un port sosesc vasele A,B,C pentru a fi încărcate. Vasul A trebuie încărcat cu 15 mii tone în maximum 48 de ore, vasul B trebuie încărcat cu 20 mii tone în maximum 60 de ore iar vasul C trebuie încărcat cu 45 mii tone în maximum 70 de ore. (timpii de staţionare pentru încărcare se numesc timpi de stalii şi sunt prevăzuţi în contractul de transport; orice depăşire a acestor timpi (contrastalii) se penalizează, penalizarea depinzând de tipul navei etc) Terminalul dispune de pompe şi conducte care însumează o capacitate de încărcare de 1200 tone pe oră. Se pune problema de a stabili ce debit trebuie afectat fiecărei nave astfel încât ele să fie încărcate în cel mai scurt timp.

Dacă se notează cu y₁ , y₂ , y₃ deditele repartizate vaselor A,B,C şi cu x₁ , x₂ , x₃ numărul de ore necesar încărcării lor se obţine uşor următorul program neliniar:

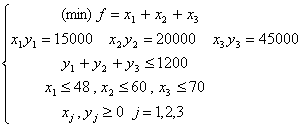
Eliminând y₁ , y₂ , y₃ rezultă modelul mai simplu:

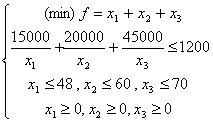
§ 3. Dificultăţi cauzate de neliniaritate

Considerăm problema de optimizare:

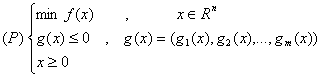
a cărei mulţime de soluţii admisibile o notăm cu A:

A =

(P) se rescrie:

Să se determine x^*ÎA cu proprietatea:

Este cunoscut faptul că dacă (P) este un program liniar (adică f şi g₁,g₂,…,g_m sunt funcţii liniare) atunci mulţimea A este convexă şi mai mult chiar poliedrală (intersecţie finită de semispaţii).Aceste proprietăţi ale mulţimii A plus faptul că funcţia obiectiv este şi ea liniară ne asigură că:

· o soluţie optimă – dacă există – este un punct de minim global adică:

f(x^*) £ f(x) (") x ÎA

· cel puţin o soluţie este un vârf al mulţimii A

Cum numărul vârfurilor mulţimii poliedrale A este finit urmează că, pentru programul liniar (P), problema determinării unei soluţii optime x^* din mulţimea, în general infinită, a tuturor soluţiilor admisibile se reduce la găsirea lui x^* în mulţimea finită a vârfurilor acestei mulţimi.

Metoda simplex realizează în mod sistematic această căutare oferind într-un număr finit de paşi (iteraţii) soluţia optimă x^*.

Neliniaritatea obiectivului sau a unora dintre restricţii face ca unele din proprietăţile relevate mai sus să dispară fapt care duce la complicarea sarcinii de determinare a optimului.

1) De la bun început vom sublinia faptul că în programarea neliniară – cu câteva excepţii – metodele de rezolvare obţin “teoretic” soluţia optimă ca limită a unui şir de soluţii. Astfel, un proces concret de optimizare neliniară este finit nu datorită structurii problemei ci prin voinţa utilizatorului care limitează numărul paşilor în funcţie de o serie întreagă de factori cum ar fi : complexitatea calcului, timpul disponibil, performanţele echipamentului de calcul etc.

2) este posibil ca funcţia obiectiv din (P) să aibe mai multe minime locale pe mulţimea soluţiilor admisibile A . Pentru exemplificare considerăm problema:

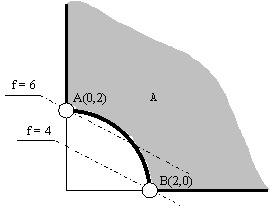
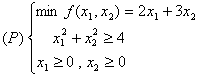
Figura 3.1

Mulţimea soluţiilor admisibile A este vizualizată în fig.3.1. Evident, A nu este o mulţime convexă. Punctul A(0,2) oferă obiectivului valoarea 6 care este cea mai mică valoare a funcţiei f pe soluţiile admisibile situate în imediata apropiere de A! Totuşi A nu este soluţia optimă a problemei (P) deoarece în B(2,0) f are valoarea 4 < 6. Ca şi A, B minimizează funcţia obiectiv pe soluţiile admisibile “vecine” cu B dar, spre deosebire de A, B minimizează obiectivul pe întreaga mulţime A şi în consecinţă reprezintă soluţia optimă a problemei (P). Spunem că A şi B sunt puncte de minim local ale funcţiei obiectiv f, B fiind chiar un punct de minim global.

Posibilitatea existenţei mai multor minime locale ale funcţiei obiectiv reprezintă o serioasă dificultate în rezolvarea unui program neliniar. Într-adevăr, prin însăşi formulare, într-o asemenea problemă se cere determinarea minimului global al obiectivului. Or, toate metodele de optimizare neliniară cunoscute, nu reuşesc să determine decât cel mult un minim local, neexistând garanţia că acesta coincide cu minimul global căutat.

După cum vom vedea, dacă A este convexă iar funcţia obiectiv este convexă şi se minimizează atunci aceasta are cel mult un minim local care – dacă există –este automat global ! Din fericire, marea majoritate a aplicaţiilor economice au proprietăţile de mai sus, fapt care constituie un serios avantaj.

3) Chiar dacă restricţiile din (P) sunt liniare dar obiectivul ramâne neliniar însă convex, soluţia optimă, deşi se află pe frontiera lui A nu este neapărat vârf. Considerăm următorul exemplu:

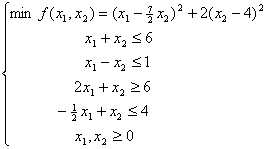
Figura 3.2

Curbele de nivel ale funcţiei obiectiv patratice f sunt elipse centrate în x^Æ = (7/2 , 4) care reprezintă şi punctul de minim nerestricţionat al lui f. Se poate arăta, prin mijloace algebrice elementare că f are pe A un minim global x^* = (5/2 , 7/2) care nu este vârf al lui A .

4) este posibil ca soluţia optimă să fie situată în interiorul mulţimii A . Pentru exemplificare să ataşăm restricţiilor din problema precedentă funcţia

al cărei minim liber este punctul x^Æ = (2 , 3). Deoarece x^Æ Î A ( şi mai precis x^Æ Î Int (A ) ) acest punct reprezintă soluţia optimă x^*.

§ 4. Clase de probleme neliniare

1) Problemele de optimizare fără restricţii au forma generală:

Să se determine x^* Î Rⁿ care minimizează valoarea funcţiei

minimul fiind luat dupa toţi x Î Rⁿ în care funcţia f este definită.

2) Probleme de optimizare cu restricţii liniare şi funcţie obiectiv neliniară. În această clasă un loc deosebit îl ocupă problemele de programare patratică în care funcţia obiectiv este un polinom de gradul doi în variabilele sale:

Importanţa problemelor de programare patratică este motivată prin:

· faptul că modelează cu suficientă acurateţe multe situaţii practice;

· se rezolvă prin metode derivate din metoda simplex într-un număr finit de paşi;

· rezolvarea multor probleme cu restricţii liniare şi funcţie obiectiv neliniară se poate reduce la rezolvarea unei secvenţe de probleme de programare patratică ale căror funcţii obiectiv aproximează din ce în ce mai bine obiectivul neliniar original.

3) Problemele de programare convexă se caracterizează prin:

· funcţie obiectiv convexă dacă aceasta se minimizează (echivalent: funcţie obiectiv concavă dacă aceasta se maximizează);

· restricţiile inegalităţi sunt de forma în care g_i este o funcţie convexă (echivalent cu g_i funcţie concavă);

· eventualele restricţii egalităţi sunt liniare, cerinţă motivată prin aceea că funcţiile liniare sunt singurele funcţii simultan convexe şi concave.

Problemele convexe au următoarele proprietăţi fundamentale:

· mulţimea soluţiilor admisibile este convexă;

· funcţia obiectiv admite cel mult un optim (minim sau maxim) local; automat acesta va fi un optim global şi va reprezenta optimul problemei;

· dacă optimul liber (nerestricţionat) al funcţiei obiectiv nu este o soluţie admisibilă atunci optimul restricţionat se găseşte cu necesitate pe frontiera mulţimii A .

Importanţa acestei clase de probleme este covârşitoare. Într-adevăr:

· programarea convexă include programarea liniară ;

· în acest domeniu a fost depus cel mai mare efort de cercetare şi s-au obţinut cele mai puternice rezultate teoretice (cum ar fi teoria dualităţii neliniare, condiţiile de optimalitate Kuhn – Tucker) şi practice (metode şi algoritmi de optimizare);

· întregul formalism matematic al teoriei economice moderne se bazează pe ipotezele de convexitate.

4)Problemele de programare separabilă se caracterizează prin faptul că funcţia obiectiv f ca şi funcţiile g_I din restricţii sunt separabile în sensul următoarei definiţii:

Funcţia se numeşte separabilă dacă ea se poate scrie ca o sumă de funcţii, fiecare de câte o singură variabilă:

Separabilitatea este importantă prin aceea că uşurează optimizarea. De exemplu, optimizarea unei funcţii separabile fără restricţii se reduce la optimizarea independentă a termenilor!

5) Problemele de programare neconvexă reunesc toate problemele care nu satisfac ipotezele de convexitate. Ele sunt “grele” în primul rând din cauza faptului că au mai multe minime locale. După cum s-a mai spus, metodele actuale pot determina un asemenea optim dar nu garantează că optimul găsit este cel global. Din fericire, există câteve tipuri de probleme neconvexe, utile în practică, care pot fi rezolvate fără dificultăţi deosebite prin metode speciale. rintre aceste tipuri, se numără problemele de programare fracţionară. Iată un exemplu:

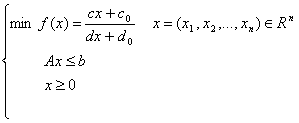
unde se presupune că pe A ={x ÎRⁿ ½½Ax £ b , x ³ 0}.

O asemenea problemă se reduce la un program liniar uzual punând:

astfel că .

Rezultă programul liniar echivalent în n + 1 variabile y = (y₁,y₂,…,y_n) şi t:

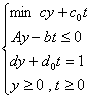
§ 5. Mulţimi şi funcţii convexe

Reamintim că o mulţime C Í Rⁿ se numeşte convexă dacă o dată cu două puncte conţine şi segmentul care le uneşte. Formal:

C este convexă

Fie C o mulţime convexă şi f o funcţie numerică definită în toate punctele mulţimii C. Spunem că f este convexă dacă:

avem:

Vom zice că f este concavă dacă funcţia opusă –f este convexă. Aceasta revine la:

Funcţia f se numeşte strict convexă (strict concavă) dacă inegalităţile de mai sus sunt stricte şi .

Exemple de funcţii convexe

1) Pentru funcţiile de o singură variabilă, convexitatea se traduce prin faptul că graficul “ţine apa”. Dacă I este un interval deschis (deci o mulţime convexă din R) şi f este o funcţie definită pe I şi care este de două ori derivabilă pe I atunci f este convexă .

2) Orice funcţie liniară de n variabile

este simultan convexă şi concavă.

3) Dacă f şi g sunt funcţii convexe cu acelaşi domeniu convex de definiţie şi a ³ 0 , b ³ 0 atunci combinaţia af + bg este deasemenea o funcţie convexă.

4)Să considerăm funcţia patratică în n variabile:

definită în întreg Rⁿ. Dacă punem:

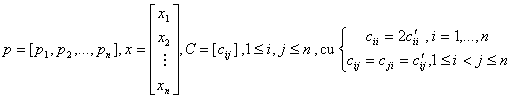
f se scrie condensat:

Notăm că prin construcţie, matricea C este simetrică.

Cercetăm în ce condiţii f este o funcţie convexă. Deoarece “partea liniară” este convexă, chestiunea se reduce la a vedea în ce condiţii funcţia “pur patratică” este convexă. Un calcul direct arată că j satisface identitatea:

Acum, dacă lÎ[0,1], identitatea precedentă echivalează convexitatea funcţiei j cu condiţia:

cerinţă care, după cum este cunoscut din algebra liniară, defineşte matricea C ca matrice pozitiv semidefinită.

Cu acelaşi raţionament conchidem că j este strict convexă dacă şi numai dacă matricea C este pozitiv definită adică:

şi

Recapitulând obţinem:

Funcţia patratică este convexă (strict convexă) dacă şi numai dacă matricea simetrică C este pozitiv semidefinită (pozitiv definită).

Reamintim că matricea simetrică este pozitiv semidefinită (pozitiv definită) dacă şi numai dacă toţi minorii care se sprijină pe diagonala principală, adică:

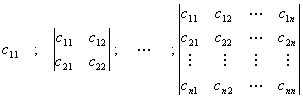
sunt ³ 0 (respectiv > 0).

6) Mai general, fie f o funcţie definită şi având derivate parţiale de ordinul doi în orice punct al unei mulţimi convexe deschise C din Rⁿ. Atunci f este convexă dacă şi numai dacă matricea hessiană

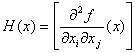
este pozitiv semidefinită, în fiecare punct x Î C. Dacă este pozitiv definită în orice punct din C, funcţia f este strict convexă.Într-adevăr să fixăm un x Î C şi un z Î Rⁿ oarecare.Considerăm funcţia de o singură variabilă:

definită pentru toţi t Î R cu proprietatea că x + tz Î C (aceşti t există cu siguranţă şi deoarece C este o mulţime deschisă, ei formează un interval deschis în R ce conţine 0). Evident, funcţia f este convexă dacă şi numai dacă funcţia g este convexă, indiferent de alegerea lui x Î C şi a lui z Î Rⁿ.Ca şi f, g este de două ori derivabilă şi

Atunci, f este convexă Û (") x Î C, (") z Î Rⁿ şi (") t Î R cu x + tz Î C, , Û H(x) este pozitiv semidefinită (") x Î C etc.

În continuare, vom justifica unele proprietăţi ale programelor convexe anunţate deja în secţiunea precedentă.

Propoziţie Fie funcţii convexe definite în toate punctele unei mulţimi convexe C Í Rⁿ. Atunci mulţimea:

A =

este convexă.

Demonstraţie Deoarece :

A = Ç … Ç

şi o intersecţie de mulţimi convexe este încă o mulţime convexă, va fi suficient să arătăm că dacă g este o funcţie convexă pe C atunci mulţimea :

A =

este convexă. Fie x,y Î A şi l Î [0,1]; atunci g(x) £0 , g(y) £0 astfel că:

Prin urmare (1-l)x + ly Î A .

Consecinţă Mulţimea soluţiilor admisibile ale unui program convex este o mulţime convexă.

Teoremă Considerăm problema de optimizare convexă: min{ f ( x )½x ÎA } în care A este mulţimea convexă a soluţiilor admisibile iar f este o funcţie convexă pe A . Dacă f are în x^* Î A un minim local atunci x^* este un punct de minim global al funcţiei f pe întreg A .

Demonstraţie Prin ipoteză, f ( x^*) £ f ( x ) oricare ar fi x Î A , suficient de aproape de x^*. Presupunem prin absurd că x^* nu este un minim global al funcţiei f : există atunci x^**Î A astfel încât f ( x^**) < f ( x^* ). Să considerăm acum un punct interior variabil pe segmentul [x^*, x^**] :

Deoarece A este convexă, toate aceste puncte sunt în A . Funcţia f fiind convexă avem:

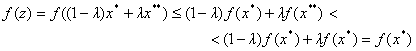
Pentru l suficient de mic, z se va afla în imediata apropiere a lui x^* şi deci, conform ipotezei, f( z ) ³ f( x^* ), în contradicţie cu cele arătate mai sus. Contradicţie ! Deci x^* este un minim global al funcţiei f.

§ 6. Optimizare fără restricţii

6.1 Introducere Fie f o funcţie numerică de n variabile pe care, pentru simplitate, o presupunem definită şi cu derivate parţiale cel puţin de ordinul doi în fiecare punct din Rⁿ. Considerăm problema de optimizare fără restricţii:

(P) Să se determine x^*ÎRⁿ cu proprietatea:

În legătură cu această problemă, analiza matematică clasică furnizează următorul rezultat fundamental:

Teoremă Dacă x^* este un punct de extrem local al funcţiei f, atunci Ñf(x^*) = 0, unde

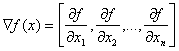(6.1)

este gradientul funcţiei f. Reciproc, dacă x^*Î Rⁿ este un punct în care condiţia (1) are loc şi în plus matricea hessiană H(x^*) este pozitiv definită, unde

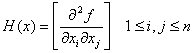
atunci x^* este un punct de minim local al funcţiei f.

Prin urmare, soluţia optimă a problemei (P) trebuie căutată printre soluţiile sistemului de n ecuaţii în n variabile, în general neliniar:

(6.2)

Însă rezolvarea sistemului (6.2), cel puţin în sensul uzual al termenului, este practic imposibil de făcut în cvasitotalitatea cazurilor practice. Chiar şi în cazul fericit în care, prin mijloace analitice – adică “cu formule” – am putea găsi o soluţie a sistemului (6.2) nu avem nici o garanţie că aceasta este soluţia optimă a problemei (P): ea ar putea fi foarte bine un punct de maxim local sau un punct şa sau, în cel mai bun caz, un minim local diferit de cel global! Astfel apare necesitatea considerării altor metode de abordare a problemei (P).

6.2 Principiul metodelor de optimizare fără restricţii Ideea comună a tuturor metodelor de minimizare nerestricţionată (liberă) este următoarea:

· Se generează un şir de puncte x⁰, x¹, x² … din Rⁿ, numite în continuare aproximaţii. Punctul iniţial x⁰ este dat, alegerea sa fiind făcută de utilizator în funcţie de specificul problemei (P). O dată obţinută aproximaţia x^k, noua aproximaţie x^k+1 se determină astfel:

· Se alege o direcţie de deplasare s^k precum şi un pas al deplasării a_k ; s^k este un vector nenul din Rⁿ – de regulă ; a_k este un scalar pozitiv.

· Se pune:

(6.3)

În principiu, vectorul s^k este astfel ales încât

prin deplasarea din x^k în direcţia s^k, să se

obţină – cel puţin în prima fază a deplasării –

o descreştere a valorii funcţiei de minimizat f.

O dată stabilită direcţia de deplasare s^k, pasul

a_k se alege astfel încât:

Figura 6.1

Prin urmare:

Mai precis a_k se găseşte prin minimizarea funcţiei de o singură variabilă:

(6.4)

Pentru a obţine o metodă efectivă de minimizare este necesar să se precizeze:

· modul de alegere a direcţiei de deplasare s^k, k = 0,1,2,…;

· modul de alegere a pasului a_k altfel spus, modul în care se execută minimizarea funcţiei unidimensionale g(a) din (6.4);

· procedeul de oprire a procesului iterativ.

Decisivă în diferenţierea metodelor concrete atât în ceea ce fundamentul teoretic cât şi performanţele numerice este prima chestiune, legată de alegerea direcţiei de deplasare.

Este foarte important de reţinut că dacă funcţia de minimizat nu are proprietăţi adiţionale “bune”, cum ar fi aceea de a fi convexă, rezultatul aplicării acestor metode se materializează în cel mai bun caz, într-un minim local – de regulă cel mai apropiat de punctul iniţial x⁰. În practică, pentru a obţine toate minimele locale şi în particular minimul global, se procedează la repetarea minimizării din mai multe puncte iniţiale, judicios alese.

Marea majoritate a metodelor de minimizare nerestricţionată presupun diferenţiabilitatea funcţiei obiectiv ; există totuşi şi scheme de minimizare pentru funcţii nediferenţiabile!

6.3 Gradientul unei funcţii. Proprietăţi În ipotezele şi notaţiile precedente, o hipersuprafaţă de nivel a funcţiei f este mulţimea punctelor care satisfac o ecuaţie de forma: f( x ) = C, unde C este o constantă. În cazul a două (respectiv trei) variabile vom vorbi despre curbe (respectiv,suprafeţe) de nivel. Astfel pentru funcţiile:

curbele de nivel sunt: a) drepte paralele; b) cercuri concentrice; c) elipse concentrice (vezi fig. 6.2)

Gradientul funcţiei f este vectorul:

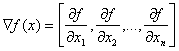
Acesta are următoarele proprietăţi:

· În orice punct de extrem local x^* al funcţiei f avem Ñf(x^*) = 0; reciproca nu este în general adevărată.

· Fie un punct în care .Atunci este direcţia de deplasare din corespunzătoare celei mai rapide descreşteri afuncţiei f. Analog, este direcţia celei mai rapide creşteri.

Într-adevăr, să considerăm o direcţie oarecare şi funcţia :

care indică variaţia funcţiei f pe direcţia de deplasare s din .

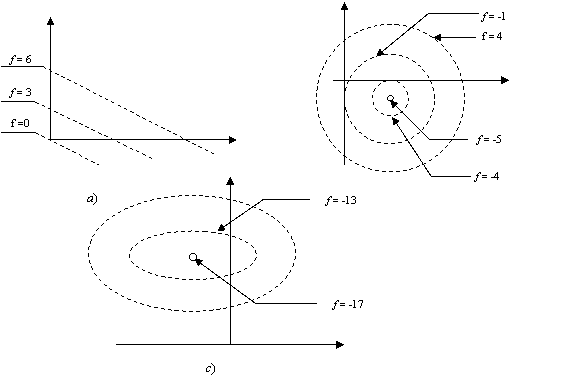
Figura 6.2

După cum se ştie, variaţia (adică creşterea sau descreşterea) potenţială sau incipientă a funcţiei f pe direcţia s plecând din , este dată de derivata .

În general:

astfel că:

Din inegalitatea Cauchy – Buniakovski – Schwarz:

rezultă că are cea mai mică valoare pentru

şi cea mai mare pentru s = .

· Dacă , atunci acest vector

este perpendicular pe hipersuprafaţa de nivel

ce trece prin 9vezi fig. 4.8

Figura 6.3

Exemplul 6.1 Considerăm funcţia patratică:

Curbele sale de nivel sunt elipse cu centrul în punctul care reprezintă şi punctulde minim global al funcţiei.Gradientul lui f:

în punctul = (1,1) este nenul: = (32,-6). Cea mai rapidă descreştere a funcţiei f plecând din are loc pe direcţia = (-32,6) – vezi fig. 6.4

Atenţie: pe direcţia celei mai rapide descreşteri, funcţia nu descreşte neîncetat! Pentru ilustrare, în exemplul de mai sus, să considerăm un punct variabil pe direcţia celei mai rapide descreşteri din = (1,1):

Pe această direcţie, comportarea funcţiei f este descrisă de funcţia:

a cărei variaţie este arătată în fig.6.5

Figura 6.4 Figura 6.5

Se observă că atunci când a creşte de la 0 la 0.032 (= punctul în care g(a) are valoarea minimă), funcţia g şi deci şi funcţia f scad de la valoarea 25 la valoarea 7.893 după care încep din nou să crească!

6.4 Criterii de oprire ale procesului iterativ de minimizare 1) Deoarece într-un punct de minim local avem Ñf(x^*) = 0, procesul de minimizare se poate opri în momentul în care:

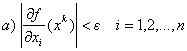
sau:

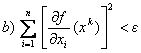
unde e este un număr pozitiv foarte mic, ca de exemplu e = 10^-5.

3) De multe ori este preferabil să oprim procesul iterativ în momentul în care variaţia funcţiei obiectiv în două aproximaţii succesive nu depăşeşte o toleranţă dată:

3) Se poate întâmpla ca, din cauza unei nefericite alegeri a aproximaţiei iniţiale x⁰ sau a structurii funcţiei de minimizat, procesul iterativ, deşi convergent, să fie foarte lent. În asemenea situaţii, timpul de calcul poate atinge valori nepermis de mari. Vom evita acest inconvenient limitând din start numărul iteraţiilor posibil de efectuat.

6.5 Minimizarea unei funcţii de o singură variabilă În secţiunea introductivă am văzut că toate metodele de minimizare nerestricţionată a unei funcţii f de mai multe variabile necesită minimizarea unei funcţii g(a) de o singură variabilă.Deoarece minimizarea unidimensională se efectuează la fiecare iteraţie a procesului de minimizare multidimensională este clar că eficacitatea procesului multidimensional depinde de calităţile procesului unidimensional.

În continuare vom presupune că în prealabil am localizat un punct de minim x^* al funcţiei g într-un interval (a,b) suficient de mic.

În general, metodele de minimizare unidimensională se bazează pe una din următoarele idei:

· Se aproximează funcţia g pe intervalul (a,b) printr-un polinom de interpolare de grad doi sau trei al cărui punct de minim din (a,b) se determină uşor pe baza unei formule. Punctul de minim astfel calculat se consideră a fi o bună aproximare a punctului de minim x^* căutat.

Construcţia polinomului de interpolare se poate face folosind:

· numai evaluări ale funcţiei g (în câteva puncte);

· evaluări atât ale funcţiei g cât şi ale derivatei sale.

De exemplu:

· putem construi un polinom de interpolare de gradul trei utilizând valorile funcţiei g şi ale derivatei sale în punctele a şi b ce “mărginesc” punctul de minim căutat.

· putem construi un polinom de interpolare de gradul doi utilizând valorile funcţiei g în a şi b precum şi într-un al treilea punct cÎ (a,b) – de obicei se ia .

· Se micşorează progresiv intervalul (a,b) la un interval care de asemenea conţine pe x^* şi a cărui lungime este inferioară unei toleranţe date:

număr foarte mic.

Atunci orice punct din aproximează x^* cu toleranţa e în sensul că:

Micşorarea intervalului (a,b) se face cu ajutorul evaluării funcţiei g şi/sau ale derivatei sale într-un număr de puncte din interiorul lui (a,b). Cele mai cunoscute metode de acest fel sunt metoda bisecţiei succesive, metoda secţiunii de aur şi metoda Fibonacci.

În figura 6.6 este prezentată schema logică a metodei bisecţiei succesive ; justificarea metodei rezultă imediat din situaţiile ilustrate în figurile 6.7a) şi 6.7b).

Pentru a înţelege modul de acţiune al metodelor bazate exclusiv pe evaluarea funcţiei de minimizat în diferite puncte sunt necesare câteva pregătiri.

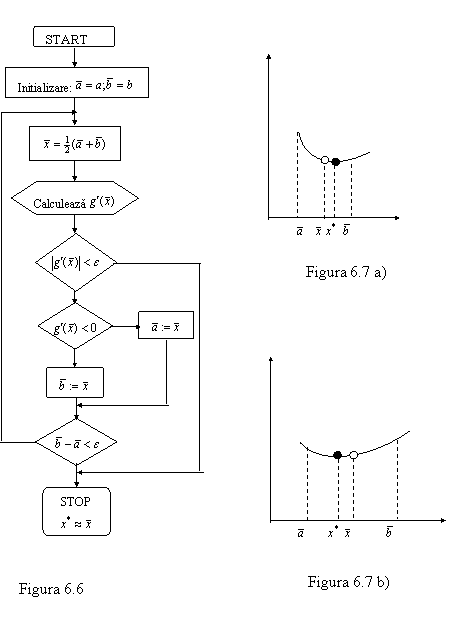
Deoarece în intervalul de localizare (a,b) am presupus că f are un unic punct de minim x* (vezi fig. 6.8) urmează că oricare ar fi x₁ < x₂ din (a,b) :

dacă

şi

dacă

Alegem două puncte x_S şi x_D în (a,b)

astfel încât x_S < x_D pe care le vom

numi puncte interioare. Dacă

,atunci cu necesitate

x^* se va afla în intervalul (a,x_D).

Figura 6.8

Dacă din contră, , atunci cu siguranţă x^* va fi în (x_S,b).Cele două situaţii sunt ilustrate în figurile 6.9a) şi 6.9b).

Figura 6.9a) Figura 6.9b)

Observăm că noul interval mai mic conţine cu necesitate unul din punctele interioare alese. Dacă în noul interval mai mic alegem încă un punct interior putem repeta consideraţiile precedente.

Metodele de minimizare unidimensională bazate pe evaluări multiple se diferenţiază prin modul de alegere a celor două puncte interioare x_S şi x_D.

Vom descrie în continuare metoda secţiunii de aur. Fie .

START. Iniţializăm:

· extremităţile intervalului curent care conţine punctul de minim x^* căutat:

· punctele interioare:

Evaluăm funcţia f în x_S şi x_D.

Conţinutul unei iteraţii:

Pasul 1. Se compară . Dacă:

· se merge la pasul 2.

· se merge la pasul 3.

Pasul 2. ( x^* se află în intervalul şi tot aici se găseşte şi x_S)

Actualizăm:

Dacă h < e se merge la pasul 4. Altminteri, actualizăm:

Evaluăm f în (noul) x_S. Ne întoarcem la pasul 1 în cadrul unei noi iteraţii.

Pasul 3. ( x^* se află în intervalul şi tot aici se găseşte şi x_D)

Actualizăm:

Dacă h < e se merge la pasul 4. Altminteri, actualizăm:

Evaluăm f în (noul) x_D. Ne întoarcem la pasul 1 în cadrul unei noi iteraţii.

Pasul 4. .

6.6 Schema logică de principiu a metodelor de optimizare nerestricţionată

Consideraţiile precedente conduc la schema logică de principiu din fig. 6.10. Elementele esenţiale ale blocurilor P (alegerea Pasului deplasării) şi O (Oprirea procesului iterativ) au fost deja discutate în secţiunile 6.4 şi 6.5.În ceea ce priveşte blocul D (alegerea Direcţiei de deplasare) acesta diferă de la metodă la metodă. Cea mai simplă metodă de minimizare nerestricţionată, datorată lui Cauchy va fi prezentată în continuare.

6.7 Metoda gradientului (Cauchy)

La fiecare iteraţie a algoritmului din fig.6.10 direcţia de deplasare este dată de relaţia:

cu condiţia ca

Această opţiune se bazează pe faptul că este direcţia celei mai rapide descreşteri din x^k.

Caracteristic acestei metode este faptul că două direcţii de deplasare consecutive sunt perpendiculare! Într-adevăr, dată direcţia s^k, lungimea pasului a_k al deplasării se află, aşa cum s-a mai spus, minimizând funcţia unidimensională:

Prin urmare .Am văzut că: - a se revedea secţiunea 6.3! – aşa încât:

Pentru funcţiile “sferice” de forma:

metoda gradientului oferă punctul de minim (global) într-o singură iteraţie, indiferent de aproximaţia iniţială x⁰ (vezi fig. 6.11a) Pentru orice altă funcţie şirul de aproximaţii:

x⁰ , x¹ , x² ,…. pentru care f(x⁰) > f(x¹) > f(x²) >…

conduce în general la un optim local.

Principalul neajuns al metodei gradientului constă în faptul că paşii succesivi sunt perpendiculari fapt care, în cazul anumitor funcţii, conduce la o convergenţă foarte lentă. Mai precis, dacă hipersuprafeţele de nivel au o oarecare “excentricitate” zig – zagul procesului iterativ amendează convergenţa,deoarece în acest caz direcţia gradientului este mult diferită de direcţia către minim (vezi fig. 6.11b)

Există scheme de minimizare mult mai eficiente dintre care cea mai puternică pare a fi metoda Davidon – Fletcher – Powell [3]. În principiu,aceste metode garantează obţinerea minimului unei funcţii patratice de n variabile în cel mult n paşi.

Exemplu numeric Vom efectua câteva iteraţii pentru căutarea minimului funcţiei:

cu metoda gradientului. Punctul de plecare x⁰ = (1,1)

Gradientul funcţiei:

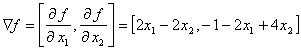
Iteraţia 1

· Ñf(x⁰) = [0,1]

· s⁰ = -Ñf(x⁰) = [0,-1]

· x(a)= x⁰ + as⁰ = [1,1] + a[0,-1] = [1,1 - a] , a > 0

· g(a) = f(x(a)) = 2a² - a are un minim în a₀ = ¼

· x¹ = x(1/4) = [1,3/4]

Iteraţia 2

· Ñf(x¹) = [1/2,0]

· s¹ = -Ñf(x¹) = [-1/2,0]

· x(a)= x¹ + as¹ = [1,3/4] + a[-1/2,0] = [1 - a/2,3/4] , a > 0

· g(a) = f(x(a)) = are un minim în a₁ = ½

· x² = x(1/2) = [3/4,3/4]

Iteraţia 3

· Ñf(x²) = [0,1/2]

· s² = -Ñf(x²) = [0,-1/2]

· x(a)= x² + as² = [3/4,3/4] + a[0,-1/2] = [] , a > 0

· g(a) = f(x(a)) = are un minim în a₂ = 1/4

· x³ = x(1/4) = [3/4,5/8]

La iteraţia 4 se obţine [5/8,5/8] ş.a.m.d. Funcţia dată este convexă (exerciţiu!) având un minim în x^* = [1/2,1/2]. În figura 6.12 se poate constata apropierea “în zig – zag” a punctelor x⁰ , x¹ , x³ … de x^*.

§ 7. Optimizarea neliniară fără restricţii. Cazul convex

Reluăm problema de optimizare generală sub forma:

(P) Să se determine x^* Î A Í Rⁿ cu proprietatea: f(x^*) = inf {f(x) , xÎ A}

unde A ,numită şi mulţimea soluţiilor admisibile ale problemei (P) este definită de o mulţime de restricţii:

g_i(x) £ 0 iÎ M = {1,2,...,m}

Pentru simplificarea expunerii, eventualele condiţii de nenegativitate x_j ³ 0 au fost incluse în blocul restricţiilor sub forma: -x_j £ 0.

Presupunem că funcţiile f şi g₁ , g₂ ,..., g_m sunt definite în întreg spaţiul Rⁿ, sunt convexe şi diferenţiabile şi cel puţin una dintre ele este neliniară, altminteri (P) ar fi un program liniar.Astfel, (P) este o problemă de programare convexă.

Reamintim că în acest context:

· A este o mulţime convexă şi închisă;

· orice minim local al funcţiei f pe mulţimea A este un minim global.

(vezi secţiunea 5)

Metodele de optimizare cu restricţii se împart în trei categorii:

1) Metode bazate pe adaptarea schemei generale de optimizare nerestricţionată la cazul prezenţei restricţiilor; aceste metode poartă numele generic de metode de gradient.

2) Metode bazate pe utilizarea funcţiilor de penalizare : rezolvarea problemei (P) se reduce la o suită (teoretic infinită) de optimizări nerestricţionate.

3) Metode bazate pe plane de secţiune; în principiu,aceste metode "aproximează" A printr-o mulţime poliedrală adică printr-o mulţime ce poate fi descrisă printr-un sistem de inegalităţi liniare; rezolvarea problemei (P) se reduce la o secvenţă (infinită) de optimizări liniare efectuate cu ajutorul algoritmului simplex.

7.1 Principiul metodelor de gradient

Aplicarea schemei generale de minimizare nerestricţionată trebuie să ţină seama de următoarele aspecte:

· de regulă soluţia optimă x^* a problemei (P) se găseşte pe frontiera lui A , adică satisface cu egalitate cel puţin una din restricţiile g_i(x) £ 0, iÎ M.

· chiar dacă se pleacă de la un punct iniţial x⁰ situat în interiorul lui A (Û g_i(x) < 0,i Î M) se ajunge relativ repede la un punct x^k situat chiar pe frontieră altfel spus care satisface cu egalitate o parte din restriţiile problemei (P):

g_i(x^k) = 0 , iÎ I Ì M

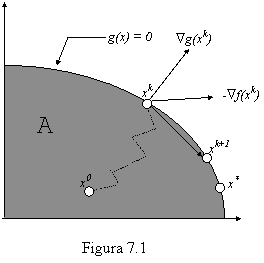
Într-o atare situaţie, direcţia celei mai rapide descreşteri -Ñf(x^k) s-ar putea să nu mai fie admisibilă adică:

(vezi fig. 7.1)

Introducem următoarea terminologie:

· o direcţie s (s Î Rⁿ, s ¹ 0) se va numi admisibilă relativ la punctul curent x^k+1 dacă o deplasare suficient de mică din x^k pe direcţia s ne menţine în A ;

· direcţia s se va numi utilizabilă dacă deplasarea din x^k pe direcţia s duce la scăderea valorii funcţiei obiectiv.

Se poate arăta că o direcţie s este admisibilă şi utilizabilă relativ la punctul curent x^k dacă şi numai dacă s satisface condiţiile:

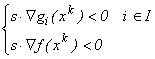(7.1)

O dată stabilită direcţia de deplasare s^k din x^k - direcţie care verifică condiţiile (7.1) - pasul a_k se alege astfel încât noua aproximaţie :

x^k+1 = x^k + a_k×s^k

să aibe proprietăţile:

x^k+1 Î A ( Û g_i(x^k+1) £ 0 , i Î M) şi f(x^k+1) < f(x^k)

Cu acest amendament - legat de modul de alegere a direcţiei de deplasare - schema generală de minimizare nerestricţionată funcţionează şi în cazul prezenţei restricţiilor.

7.2 Principiul metodelor bazate pe funcţii de penalizare

În esenţă, aceste metode încorporează restricţiile problemei (P0 în funcţia obiectiv prin intermediul unei funcţii care penalizează nerespectarea lor.

Pentru ilustrare să considerăm funcţia:

al cărei grafic este dat în fig 7.2. Considerăm problema de minimizare fără restricţii:

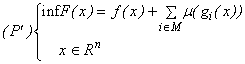
Evident:

În consecinţă,orice procedeu de minimizare a funcţiei F se va orienta către punctele mulţimii A şi deci va minimiza funcţia originală f. Dificultatea majoră rezidă în faptul că funcţia de penalizare m are o discontinuitate în 0 care atrage după sine discontinuitatea funcţiei F pe frontiera lui A ! Cum de regulă punctul de optim x^* se află pe frontieră, metodele de minimizare bazate pe gradient nu sunt aplicabile deoarece gradientul funcţiei F nu este definit pe frontiera lui A .

Totuşi ideea de a adăuga un termen la expresia funcţiei f care să penalizeze o eventuală "ieşire" din A şi de a minimiza "liber" funcţia rezultată poate fi salvată utilizând în locul funcţiei m o funcţie mai puţin "rigidă" care să aibe proprietăţile de regularitate (continuitate, diferenţiabilitate) reclamate de utilizarea metodelor de gradient. Un exemplu ar putea fi funcţia:

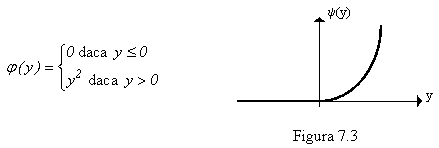
cu ajutorul căreia construim problema de minimizare fără restricţii

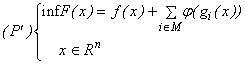
Acum,penalizarea pentru ieşirea în afara mulţimii A nu mai este "infinită" astfel că soluţia optimă a problemei (P') ar putea să nu fie în A , altfel spus ar putea încălca unele restricţii.Pentru a diminua aceste încălcări amplificăm efectul penalizării înmulţind termenul de penalizare cu o constantă r > 0 suficient de mare. (P') devine:

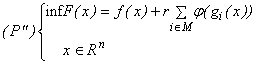
Introducerea multiplicatorului r măreşte excentricitatea hipersuprafeţelor de nivel ale funcţiei F; or, este ştiut că excentricitatea pronunţată influenţează negativ viteza de convergenţă a tuturor algoritmilor de minimizare nerestricţionată.

Dificultăţile semnalate au condus la următoarea schemă de lucru. În locul rezolvării unei singure probleme de minimizare fără restricţii se va rezolva o secvenţă de asemenea probleme. Concret, se începe rezolvarea problemei (P'') cu o constantă r₀ nu prea mare; fie x⁰ soluţia optimă. Dacă x⁰ Ï A se reia (P'') cu un multiplicator r₁ > r₀ utilizând x⁰ ca aproximaţie iniţială. Fie x¹ noua soluţie optimă. Dacă nici x¹ Ï A schimbăm r₁ cu r₂> r₁ etc. Se poate arăta că dacă r_k ® ¥ atunci şirul x⁰ , x¹ , x² ...converge către soluţia optimă a problemei cu restricţii (P).

Să observăm că soluţiile intermediare x⁰ , x¹ , x² ... nu sunt admisibile şi din acest punct de vedere metoda descrisă seamănă cu algoritmul simplex dual din programarea liniară. Acest fapt poate fi un serios dezavantaj deoarece dacă pentru anumite restricţii nu sunt permise nici cele mai mici încălcări atunci nici o soluţie intermediară nu poate fi reţinută în caz de oprire a procesului iterativ.

§8 Condiţiile de optimalitate Kuhn - Tucker în programarea convexă

8.1 Formularea condiţiilor

Considerăm un program convex (P) pe care îl presupunem adus la următoarea formă zisă canonică:

Să se determine x^* Î Rⁿ cu proprietatea:

f(x^*) = min f(x)

(P) minimul fiind luat după toţi x Î Rⁿ care satisfac restricţiile:

g_i(x) £ 0 i = 1,...,m

şi condiţiile de nenegativitate:

x ³ 0 Û x_j ³ 0 j = 1,...,n

Pentru simplitatea expunerii vom presupune că funcţiile convexe f şi g₁ , g₂ ,..., g_m sunt definite şi diferenţiabile în întreg spaţiul Rⁿ.

Asociem fiecărei restricţii g_i(x) £ 0 o variabilă nenegativă u_i şi construim funcţia:

Funcţia L se numeşte lagrangianul problemei (P) iar u₁ , ... ,u_m se numesc multiplicatori Lagrange. Se observă imediat că pentru xÎRⁿ fixat L este o funcţie liniară în u₁ ,..., u_m iar pentru u ³ 0 fixat în R^m, L este o funcţie convexă şi diferenţiabilă.

Vom presupune îndeplinită următoarea condiţie, numită condiţia de regularitate Slater:

Există cu proprietatea că şi altfel spus, mulţimea soluţiilor admisibile A = { xÎRⁿ êg_i(x) £ 0 , x ³ 0} are interiorul relativ nevid.

Cu aceste pregătiri putem enunţa următoarea:

Teoremă (Kuhn - Tucker) Condiţia necesară şi suficientă ca x^*ÎRⁿ să fie o soluţie optimă a problemei (P) este să existe u^* ÎR^m astfel încât cuplul (x^*,u^*) să verifice relaţiile:

		i = 1,...,m j = 1,...,n
xj ³ 0 (3)	ui ³ 0 (3')

Condiţiile încadrate sunt cunoscute sub numele de condiţiile de optimalitate Kuhn - Tucker.

Deşi este un rezultat de factură pur teoretică, teorema de mai sus este la baza multor algoritmi eficienţi de rezolvare a programelor neliniare convexe cum sunt, de exemplu, cei utilizaţi în programarea patratică.

Observaţie : Condiţia de regularitate Slater intervine în probarea suficienţei condiţiilor de optimalitate K- T. Ea nu mai este necesară în cazul în care restricţiile programului (P) sunt liniare.

Exemplul 8.1 Considerăm programul neliniar patratic:

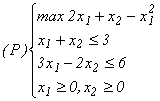
a cărui formă canonică este:

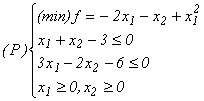
Fig. 8.1 confirmă faptul că (P) este un program convex: mulţimea soluţiilor admisibile este convexă, chiar poliedrală fiind definită prin inecuaţii liniare iar curbele de nivel f(x) = c(onstant) sunt parabole cu axa de simetrie comună x = 1. Desenul sugerează că soluţia optimă x^* satisface cu egalitate restricţia x₁ + x₂ £ 3 şi cu inegalitate strictă cealaltă restricţie şi condiţiile de nenegativitate.Aceste concluzii "calitative" şi condiţiile de optimalitate K - T ne vor permite să determinăm punctul x^*.

Asociem celor două restricţii variabilele nenegative u₁ şi u₂ şi construim lagrangianul:

L = -2x₁ - x₂ + x₁² + u₁(x₁ + x₂ - 3) + u₂(3x₁ - 2x₂ - 6)

Scriem condiţiile de optimalitate K - T:

Reamintim interpretarea acestor condiţii: este soluţia optimă a programului (P) dacă şi numai dacă există astfel încât cuplul să satisfacă relaţiile mai sus scrise.

Deoarece la optim avem: x₁ > 0 , x₂ > 0 şi 3x₁ - 2x₂ < 6 din relaţiile (1.1') , (1.2') şi (2.2') obţinem:

-2 + 2x₁ +u₁ + 3u₂ = 0 , -1 + u₁ - 2u₂ = 0 şi u₂ = 0 care împreună cu x₁ + x₂ = 3 constituie un sistem de patru ecuaţii cu patru variabile x₁ , x₂ , u₁ , u₂. Rezultă uşor:

de unde .

8.2 Condiţiile Kuhn - Tucker în programarea liniară

Evident, orice program liniar este un program convex şi ca urmare teorema de optimalitate Kuhn - Tucker funcţionează şi pentru programele liniare. După cum vom vedea , în acest caz teorema amintită se suprapune peste un rezultat fundamental al dualităţii liniare.

Să considerăm un program liniar în formă canonică de maximizare (în notaţiile uzuale):

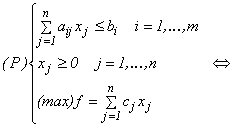
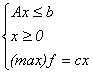
Rescriem (P) în forma canonică în care am studiat programele convexe şi asociem celor m restricţii variabilele u₁ , u₂ ,..., u_m:

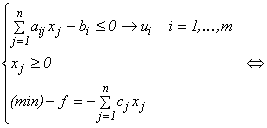
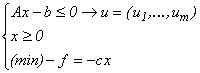
Lagrangianul problemei (P) are expresia:

Condiţiile de optimalitate K - T:

se interpretează astfel:

este o soluţie optimă a programului (P) dacă şi numai dacă există astfel încât cuplul să verifice relaţiile mai sus scrise.

Observăm că relaţiile (2_i) i = 1,...,m şi (3) definesc x^* ca soluţie admisibilă a problemei (P) în timp ce relaţiile (1_j) j = 1,...,n şi (3') definesc u^* ca soluţie admisibilă a problemei duale:

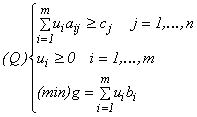Û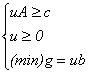

Obţinem următoarea reformulare a relaţiilor K - T:

Condiţia necesară şi suficientă ca soluţia admisibilă a problemei (P) să fie o soluţie optimă este să existe o soluţie admisibilă a problemei duale (Q) astfel încât cuplul (x^*,u^*) să verifice relaţiile:

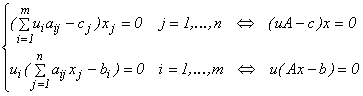
Am regăsit teorema ecarturilor complementare din teoria dualităţii liniare.

8.3 Condiţiile de optimalitate Kuhn - Tucker în programarea patratică

Considerăm problema de programare patratică:

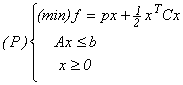
în care:

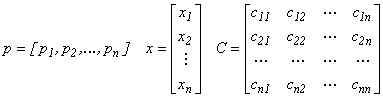= matrice simetrică

Vom presupune că matricea C este pozitiv semidefinită ; ştim atunci că funcţia patratică f este convexă şi ca urmare, programul (P) este convex.

Asociem blocului de restricţii Ax - b £ b vectorul (linie) de multiplicatori Lagrange u = [u₁,u₂,...,u_m] şi construim lagrangianul problemei (P):

În scriere matricială, condiţiile de optimalitate K - T pentru programul (P) arată astfel:

x ³ 0 (3)	u ³ 0 (3')

Transformăm inegalităţile (1) şi (2) în egalităţi introducând vectorii de variabile de abatere:

şi

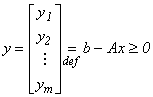
Atunci:

şi Ax+y = b

Se vede uşor că:

Cu aceste pregătiri putem formula următoarea interpretare a relaţiilor K - T:

Condiţia necesară şi suficientă pentru ca x^* Î Rⁿ să rezolve programul patratic (P) este să existe astfel încât să verifice relaţiile:

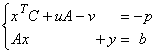(4) Û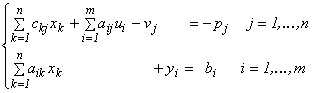

x ³ 0 , u ³ 0 , v ³ 0 , y ³ 0 Û x_k ³ 0 , u_i ³ 0 , v_j ³ 0 , y_i ³ 0

v×x = 0 ; u×y = 0 (5) Û v_jx_j = 0 j = 1,...,n ; u_iy_i = 0 i = 1,...,m

Se observă că (4) este un sistem liniar cu m + n ecuaţii şi 2m + 2n variabile. În concluzie:

Rezolvarea programului patratic (P) s-a redus la determinarea unei soluţii admisibile (adică nenegative) a sistemului liniar (4) care să verifice relaţiile de complementaritate (5).

În principiu, aceasta se poate face cu ajutorul algoritmului simplex în felul următor:

· se înmulţesc cu -1 acele egalităţi din (4) ai căror termeni liberi sunt < 0;

· dacă, după efectuarea operaţiei precedente, matricea sistemului (4) nu conţine o submatrice unitate de ordinul m + n, ea se completează cu coloanele care lipsesc adăugând - acolo unde este cazul - variabile artificiale nenegative.Astfel, sistemul (4) devine:

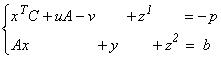
unde:

şi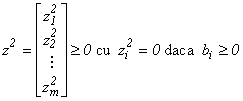

· se rezolvă programul liniar:

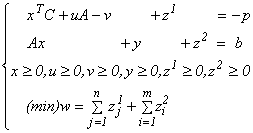
cu ajutorul algoritmului simplex, modificat cu următoarea regulă suplimentară care se referă la criteriul de intrare în bază:

La fiecare iteraţie, noua variabilă bazică va fi astfel aleasă încât:

· variabilele v_j şi x_j să nu fie simultan bazice j=1,...,n;

· variabilele u_i şi y_i să nu fie simultan bazice i=1,...,m.

La start se va pleca cu soluţia:

x = 0 , u = 0

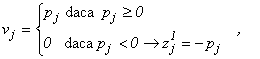
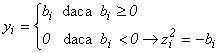
Deoarece x = 0 , u = 0 ,relaţiile de complementaritate (5) sunt verificate. Regula suplimentară ne asigură că la fiecare iteraţie:

v_j = 0 sau x_j = 0 deci v_jx_j = 0 j = 1,...,n

u_i = 0 sau y_i = 0 deci u_iy_i = 0 i = 1,...,m

Se poate arăta că dacă programul (P) este compatibil atunci într-un număr finit de iteraţii se ajunge la o soluţie în care (min)w = 0 Û toate variabilele artificiale introduse au valoarea zero. Este clar atunci că s-a obţinut o soluţie admisibilă a sistemului (4) care satisface relaţiile de complementaritate (5). Componenta x^* a acestei soluţii constituie soluţia optimă a programului patratic (P).

Observaţie Consideraţiile de mai sus constituie o descriere de principiu a algoritmului lui Wolfe pentru rezolvarea programelor patratice convexe.

Exemplu numeric Vom arăta cum se aplică efectiv condiţiile de optimalitate K - T şi algoritmul simplex la rezolvarea programului patratic:

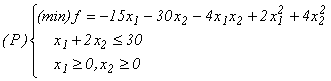
Scriem matricial funcţia obiectiv:

Matricea simetrică este chiar pozitiv definită astfel că f este o funcţie strict convexă. Lagrangianul problemei:

Condiţiile de optimalitate K - T:

x1 , x2 ³ 0	u ³ 0

Punem:

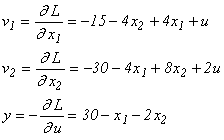
Condiţiile K - T în forma (4) - (5):

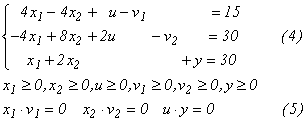
Ştim că dacă este o soluţie admisibilă a sistemului (4) care satisface relaţiile (5) atunci x^* este o soluţie optimă a problemei date.

Introducem variabilele artificiale z₁ şi z₂ în primele două egalităţi şi rezolvăm programul liniar:

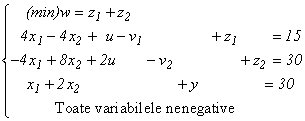
cu ajutorul algoritmului simplex, plecând de la soluţia de bază iniţială:

care satisface vizibil condiţia (5).

			0	0	0	0	0	0	1	1
CB	VB	VVB	x1	x2	u	v1	v2	y	z1	z2
1	z1	15	4	-4	1	-1	0	0	1	0	ITERAŢIA 1 Poate intra x2
1	z2	30	-4	8	2	0	-1	0	0	1	deoarece v2 = 0
0	y	30	1	2	0	0	0	1	0	0
	w	45	0	4	3	-1	-1	*	*	*
1	z1	30	2	0	2	-1	-1/2	0	1	1/2	ITERAŢIA 2 Poate intra x1
0	x2	15/4	-1/2	1	1/4	0	-1/8	0	0	1/8	deoarece v1 = 0
0	y	45/2	2	0	-1/2	0	1/4	1	0	-1/4
	w	30	2	*	2	-1	-1/2	*	*	-1/2
1	z1	15/2	0	0	5/2	-1	-3/4	-1	1	3/4	ITERAŢIA 3 Poate intra u
0	x2	75/8	0	1	1/8	0	-1/16	1/4	0	1/16	deoarece y = 0
0	x1	45/4	1	0	-1/4	0	1/8	1/2	0	-1/8
	w	15/2	*	*	5/2	-1	-3/4	-1	*	-1/4
0	u	3
0	x2	9	Nu mai este cazul!
0	x1	12
	w	0

Prin urmare,o soluţie a condiţiilor de optimalitate K - T este x^* = (12,9) şi u^* = 3.În concluzie

este o soluţie optimă a programului patratic dat de altfel şi singura având în vedere faptul că funcţia obiectiv f este strict convexă.

§ 9. Întrebări şi probleme

1. Se dă o funcţie numerică f definită în toate punctele unei mulţimi C Í Rⁿ.

a) Ce înseamnă că mulţimea C este convexă? Presupunând C convexă, ce înseamnă că funcţia f este convexă (strict convexă)?

b) Ce înseamnă că punctul x^* Î C este un punct de minim local al funcţiei f? Dar că x^* este un punct de minim global al funcţiei f pe C?

c) Arătaţi că dacă C este o mulţime convexă iar f este o funcţie strict convexă atunci f nu poate avea decât cel mult un punct de minim global pe C.

2. a) Se consideră funcţia patratică j(x) = x^TCx , x Î Rⁿ unde C este o matrice simetrică de ordinul n. Să se arate că pentru orice x,y Î Rⁿ şi orice l Î R are loc identitatea:

j((1 - l)x + ly) = (1 - l)j(x) + lj(y) - l (1 - l)j(x - y)

b) Scrieţi funcţia patratică:

în formatul matricial 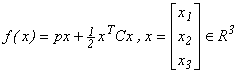şi cercetaţi dacă f este o funcţie convexă (strict convexă)

3. Descrieţi principiul metodelor de minimizare fără restricţii

4.Elaboraţi programe de calculator pentru metodele de minimizare unidimensională prezentate în secţiunea 6.5

5. Se dă funcţia patratică .

a) Scrieţi f în formatul matricial şi arătaţi că f este o funcţie strict convexă.

b) Calculaţi gradientul Ñf şi determinaţi minimul liber x* al funcţiei f.

c) Determinaţi direcţia celei mai rapide descreşteri a funcţiei f din x⁰ = (0,0) şi prima aproximaţie x¹ din metoda gradientului.

d) Efectuaţi încă două iteraţii din metoda gradientului pentru minimizarea nerestricţionată a funcţiei f. Comparaţi x³ cu x^* obţinut la b).

6. În procesul de minimizare nerestricţionată a unei funcţii numerice de trei variabile ,efectuat cu metoda gradientului,printre direcţiile de deplasare s-au numărat şi vectorii s = (1,1,-3), s' = (2,-1,1). Este posibil ca cele două direcţii să fi fost obţinute în două iteraţii consecutive?

7. Se consideră programul convex:

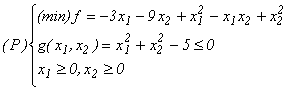
şi punctul aflat pe frontiera mulţimii soluţiilor admisibile (deoarece )

a) Calculaţi gradienţii funcţiilor f şi g în .

b) Ce condiţii trebuie să satisfacă un vector s = (s₁,s₂) Î R² pentru a fi o direcţie admisibilă şi utilizabilă din ? Care din următorii vectori s¹ = (-1,1) , s² = (1,1) , s³ = (1,-1) satisfac aceste condiţii?

8. Se dă programul neliniar patratic:

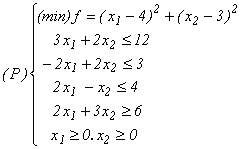
a) Vizualizaţi mulţimea soluţiilor admisibile;

b) Ce formă au curbele de nivel ale funcţiei obiectiv? Stabiliţi punctul de minim liber x^Æ al funcţiei f;

c) Scrieţi condiţiile de optimalitate Kuhn - Tucker;

d) Stabiliţi cu aproximaţie poziţia soluţiei optime x^* a programului (P) şi folosind condiţiile K - T determinaţi efectiv x^*.

9. Se dă programul neliniar;

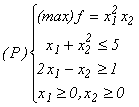
a) Reprezentaţi grafic mulţimea soluţiilor admisibile şi curbele de nivel f(x) = 1 , f(x) = 4 ale funcţiei obiectiv;

b)Aduceţi programul (P) la forma canonică şi scrieţi condiţiile de optimalitate K - T;

c)Determinaţi soluţia optimă x^* a programului (P) ştiind că ea satisface cu egalitate numai prima restricţie a acestuia.

10. În modelarea unui proces de stocare cu două produse şi spaţiu de depozitare limitat s-a ajuns la următorul program neliniar:

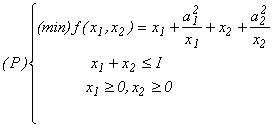
unde a₁ , a₂ , I > 0 sunt constante.

a) Să se arate că f este o funcţie convexă pe domeniul {(x₁,x₂) Î R² ê x₁ > 0 , x₂ > 0};

(se va observa că f este separabilă şi se va cercete convexitatea componentelor)

b) Scrieţi condiţiile de optimalitate K - T pentru programul convex (P);

c) Determinaţi soluţia optimă a programului (P). Discuţie.

11. Să se rezolve programul patratic:

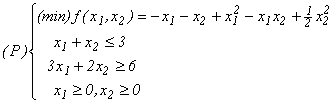
folosind condiţiile de optimalitate K - T şi algoritmul simplex (vezi secţiunea 8.2)