C A P I T O L U L III
PROBLEME DE OPTIMIZARE DE DIMENSIUNI MARI
§1. Problema dimensiunii în rezolvarea efectivă a problemelor de optimizare practice
Principala cauză generatoare de dificultăți în rezolvarea problemelor de optimizare reale este dimensiunea: o asemenea problemă este pur și simplu "prea mare". În programarea matematică, mărimea unei probleme este o chestiune relativă, depinzând de mulți parametri cum ar fi:
· numărul de variabile și numărul de restricții;
· complexitatea expresiilor funcției obiectiv și a restricțiilor;
· performanțele echipamentului de calcul: hardware și software.
Utilizarea modelelor matematice în studiul unor situații reale - în special din domeniul economic - a condus la programe matematice care suprasolicită și cele mai puternice calculatoare.Din fericire, marea majoritate a problemelor de optimizare "mari" au o "structură specială" care, în programarea liniară de exemplu, înseamnă:
· densitate mică a constantelor numerice nenule;
· gruparea elementelor nenule în blocuri așezate "pe diagonală";
· număr foarte
mare de variabile și relativ
puține restricții sau invers, multe restricții și puține variabile.
Trebuie spus că dacă un program liniar mare nu are o structură specială, sarcina colectării datelor este practic aproape imposibil
de realizat; astfel pentru un program cu 104 restricții și 106 variabile, matricea
coeficienților
ar avea 1010 intrări și în cazul unei densități de 100% ar necesita 1010 date
numerice de adunat, sortat și prelucrat!!
Pentru
programele neliniare, complexitatea și structura specială se caracterizează mult mai greu.
§2. Clasificarea metodelor de rezolvare a
programelor liniare mari
În principiu metodele de rezolvare a
programelor mari se împart în două categorii:
· metode directe: acestea specializează o procedură generală adaptând-o la specificul unei anumite clase de
probleme de optimizare.
Exemplul
tipic îl
constituie algoritmul simplex; este știut că principala problemă de calcul care apare în aplicarea lui o constituie modul de manipulare a inversei bazei
curente. În
cazul unei "structuri speciale" este posibil ca dimensiunea acestei
matrici să
se reducă
semnificativ.
Să considerăm cazul unui program liniar cu variabile superior mărginite:
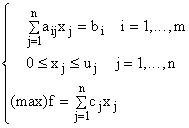
Abordarea "clasică" presupunea transformarea condițiilor de limitare superioară în egalități:
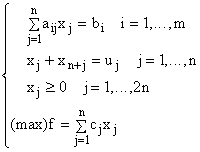
Rezulta un program cu m+n restricții și 2n variabile, ale cărui baze erau matrici de ordinul m+n.
Totuși forma particulară a restricțiilor de limitare superioară a putut fi exploatată eficient într-o specializare a algoritmului simplex în care inversa bazei curente are
dimensiunea egală
cu numărul
m al restricțiilor
propriu zise.
· metode indirecte, bazate pe descompunerea
problemei mari în
subprobleme mai mici, interconectate. Subproblemele pot fi
rezolvate independent (și dacă este posibil chiar simultan) dar faptul că ele interacționează implică existența unui mecanism (problemă) de coordonare.
Astfel, rezolvarea problemei originale mari se face "la două nivele":
· la primul nivel - inferior - se rezolvă subproblemele; rezultatele sunt
"comunicate":
· la al doilea nivel - superior - care
"analizează"
aceste rezultate și transmite nivelului inferior noi parametri.
La nivelul unu are loc o reluare a calculelor
(reoptimizare); noile rezultate sunt
trimise nivelului superior care le
analizează ș.a.m.d.
Important este faptul că acest proces iterativ este convergent în sensul că într-un număr finit
de pași
(º dialoguri între cele două nivele), nivelul coordonator "anunță" găsirea soluției optime.
§3. Descompunere în programarea liniară. Principiu
Considerăm
un program liniar în formă standard:
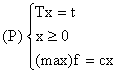 în care:
în care:
T
º matrice mŽn;
x
º coloana celor n variabile;
t
º coloana celor m termeni liberi;
c º linia celor n coeficienți din funcția obiectiv.
Pentru moment, nu vom face nici o ipoteză asupra "mărimii" programului (P) sau asupra
structurii sale. Știm că (P) poate fi rezolvat "dintr-o dată" cu ajutorul algoritmului simplex.
Ne propunem să
arătăm cum poate fi rezolvat (P) prin descompunerea sa în mai multe subprobleme mai mici, intercorelate.
Vom
împărți sistemul Tx=t al restricțiilor în două blocuri (partiționarea este deocamdată arbitrară):

· blocul Ax=b cu m1 < m
restricții;
· blocul Mx=d cu m2 =m - m1
restricții
Considerăm mulțimea soluțiilor admisibile ale
sistemului liniar Ax=b:
A ={x Î Rn | Ax = b , x ³ 0}
Este bine cunoscut faptul că A este o mulțime convexă și
chiar poliedrală (adică
o intersecție
finită
de semispații
din Rn). Ea are un
număr finit de vârfuri v1,v2,...,vs care se identifică cu soluțiile admisibile de bază ale sistemului Ax = b.
Pentru
simplitatea expunerii, vom presupune în continuare că
mulțimea
A este mărginită (această
ipoteză
este îndeplinită în mai toate cazurile practice).
Un
rezultat clasic al analizei convexe arată că orice punct al mulțimii poliedrale și mărginite A se
scrie ca o combinație convexă a vârfurilor
ei:
![]()
unde:
![]() și
și
![]()
Înlocuind ![]() în
blocul Mx = d și
în
funcția
obiectiv f = cx obținem:
în
blocul Mx = d și
în
funcția
obiectiv f = cx obținem:
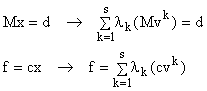
Cu notațiile:
![]()
programul (P) se scrie echivalent:
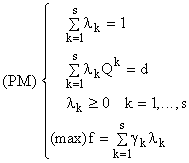 în care variabilele sunt scalarii
în care variabilele sunt scalarii ![]()
Dacă ![]() este o soluție optimă a programului (PM) atunci
este o soluție optimă a programului (PM) atunci ![]() este o soluție optimă a programului original (P).
este o soluție optimă a programului original (P).
Programul (PM) se numește program coordonator (master program) și are următoarele proprietăți:
· are mai puține restricții decât (P): doar 1+m2 față de
m1 + m2 ;
· are în general un număr foarte mare de variabile, câte una pentru fiecare vârf al mulțimii A și, după cum se știe numărul acestor vârfuri estte de obicei
"impresionant";
·
rezolvarea
programului (PM) necesită - cel puțin la prima vedere - cunoașterea vârfurilor v1,v2,...,vs fără de care nu se pot evalua colanele Qk
și
scalarii ![]() . Or, cunoașterea apriorică a vârfurilor
v1,v2,...,vs este o sarcină
extrem de grea și
practic imposibil de făcut în mai toate cazurile!
. Or, cunoașterea apriorică a vârfurilor
v1,v2,...,vs este o sarcină
extrem de grea și
practic imposibil de făcut în mai toate cazurile!
Din fericire, rezolvarea programului (PM) nu necesită cunoașterea apriorică a vârfurilor v1,v2,...,vs. După cum vom vedea în secțiunea 5, pe parcursul aplicării algoritmului simplex acestui program, vârfurile mulțimii A absolut necesare în optimizare vor fi generate (calculate) "la cerere" prin rezolvarea unor programe liniare de forma:
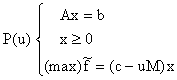
în care u este un vector linie ale cărui componente se stabilesc și se modifică în funcție de stadiul rezolvării programului (PM).
În esență, rezolvarea programului original (P) s-a
redus la:
· rezolvarea programului coordonator (PM);
și la:
· rezolvarea mai multor probleme de forma
P(u)
toate de dimensiuni mai mici decât cele ale programului (P); vezi figura
3.1

Figura 3.1
Cele
de mai sus constituie esența principiului
de descompunere Dantzig - Wolfe. El poate fi folosit atunci când programul (P) are un număr foarte
mare de restricții. Descompunerea devine și mai atractivă în cazul în care submatricea A are o structură diagonală

Figura 3.2
în care A1,A2,...,Ap
sunt matrici de diferite dimensiuni.Pentru simplificarea expunerii să presupunem că A are doar două blocuri A1 și A2. Elementele constitutive
ale programului (P) pot fi partiționate astfel:
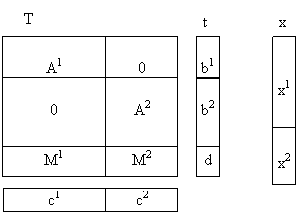
A ![]()
![]() b
b
M ![]()
Figura 3.3
Programul (P) are deci forma:
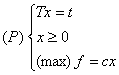 Û
Û 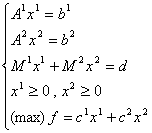
Se observă ușor că în această situație, problema P(u) se sparge în două subprobleme independente (care pot fi rezolvate simultan!):
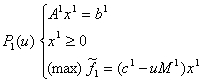
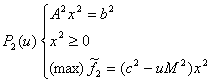
Schema de rezolvare la două nivele a programului (P) din figura 3.1
devine:
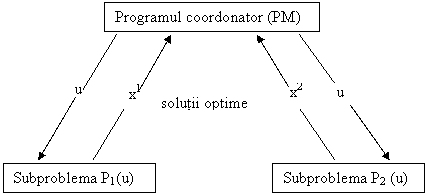
Nivel 2
Nivel 1
Figura 3.4
§4. O interpretare economică a principiului de descompunere
Să considerăm o economie
cu mai mulți agenți. Fiecare agent operează un număr de activități de pe urma cărora obține un venit. Operarea activităților implică utilizarea unor resurse disponibile în cantități limitate.
Firește,
obiectivul fiecărui
agent este maximizarea venitului
propriu.
Este clar că dacă fiecare agent ar deține controlul asupra tuturor resurselor
necesare lui atunci maximizarea venitului la
scara întregii economii s-ar
reduce la maximizarea venitului fiecărui agent în parte.
În realitate lucrurile stau altfel.
Fiecare agent deține controlul asupra anumitor resurse: capacități proprii de producție, forța de muncă angajată, resurse financiare proprii, unele
materii prime utilizate în exclusivitate.Acestea vor fi numite resurse specifice.
Pe lângă resursele specifice, fiecare agent
utilizează și
alte resurse care nu sunt la dispoziția sa exclusivă; aceste resurse sunt procurate de pe piață, la concurență cu ceilalți agenți, datorită faptului că sunt disponibile în cantități limitate. Acestea vor fi denumite resurse comune.
În acest context, problema principială care se pune este de a stabili cum vor fi
repartizate resursele comune între agenți astfel încât, la scara întregii economii, venitul să fie maxim.
Într-o economie centralizată, repartizarea
resurselor comune este făcută de stat
care indică
fiecărui
agent ce și
cât
să
producă.
Ne propunem să arătăm cum se face repartizarea comune într-o economie descentralizată în care autoritatea centrală nu mai deține controlul asupra acțiunilor agenților.
Ne vom situa în cazul ideal al unei economii liniare,
caracterizate prin următoarele ipoteze:
· pentru fiecare activitate, consumurile de
resurse și
venitul sunt direct proporționale cu nivelul la care este operată activitatea;
· nivelul de operare al unei activități poate fi reprezentat de orice număr real nenegativ;
· veniturile agenților nu se condiționează reciproc și sunt egale cu suma veniturilor activităților fiecăruia. Venitul la scara întregii economii este suma veniturilor
agenților.
Pentru
simplitatea expunerii vom presupune că în economia studiată există numai doi agenți.
Introducem notațiile:
x1, x2 º vectorii (coloană) nivelelor de operare ale activităților celor doi agenți;
b1 , b2 º vectorii (coloană) cantitățîlor disponibile din resursele specifice;
A1, A2 º matricile consumurlor unitare de resurse specifice;
M1, M2 º matricile consumurilor unitare din resursele comune;
d º vectorul (coloană) cantităților disponibile de resurse comune;
c1,
c2 º
vectorii (linie) veniturilor unitare corespunzătoare celor doi agenți.
Evident, nivelele de operare ale activităților agenților sunt condiționate de disponibilele de resurse specifice:
A1x1 £ b1 A2x2 £ b2 (4.1)
și în plus:
x1 ³ 0 x2 ³ 0
(4.2)
Vectorii x1,
x2 care satisfac relațiile 4.1 - 4.2 se vor numi programe posibile de activitate.
Un
cuplu de programe posibile (x1, x2) devine realizabil numai dacă necesarul de resurse comune se încadrează în disponibilul dat adică:
M1x1 + M2x2 £ d
(4.3)
Venitul total pe economie are expresia:
f = c1x1 +c2x2 (4.4)
Reunind (4.1 - 4.4) obținem programul liniar:
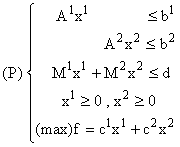 (4.5)
(4.5)
care modelează problema repartizării resurselor comune în vederea maximizării venitului pe întreaga economie.
Observăm că matricea programului (4.5) are structura bloc diagonală cu restricții de cuplare, identică cu structura pe care s-a prezentat, în secțiunea precedentă, principiul de descompunere Dantzig - Wolfe.
Din punct de vedere formal, problema
repartizării
resurselor comune într-o economie descentralizată înseamnă rezolvarea programului (P) în condițiile în care nici agenții nici autoritatea centrală nu au informații complete asupra acestuia. Astfel:
agentul
1 controlează
(cunoaște) b1, A1, M1,
c1;
agentul
2 controlează
(cunoaște) b2, A2, M2,
c2;
autoritatea
centrală
controlează
(cunoaște)
d.
Maximizarea venitului fiecărui agent, ținând seama numai de resursele sale
specifice, revine formal la rezolvarea programelor:
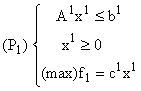
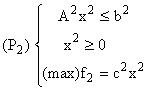
dar nu rezolvă problema repartizării resurselor comune deoarece, dacă ![]() și
și ![]() sunt soluțiile optime ale programelor din (4.6),
este posibil ca:
sunt soluțiile optime ale programelor din (4.6),
este posibil ca:
![]()
![]() £ d
£ d
În continuare vom arăta - în principiu - cum poate fi rezolvat programul (P) din (4.5) în situația în care nici autoritatea centrală și nici agenții nu dețin informații complete asupra programului!
Vom presupune că:
· între autoritatea centrală și agenți există o cooperare în sensul unui schimb de informații privind "intențiile"de acțiune;
· autoritatea centrală își asumă rolul de arbitru în următorul sens: ea "anunță" un sistem de prețuri pe resursele comune iar agenții iau aceste pețuri ca date și își diminuează veniturile cu valoarea resurselor comune solicitate.Fie u vectorul (linie) al acestor prețuri.Atunci:
· agentul 1, pentru susținerea unui program posibil x1
(posibil º A1x1
£ b1, x1 ³ 0),va trebui să "plătească" valoarea uM1x1
astfel că
venitul său
"net" va fi:
![]()
· analog, venitul agentului 2, rezultat din
programul posibil x2 (A2x2 £ b2, x2 ³ 0), va fi:
![]()
Maximizarea acestor venituri nete înseamnă rezolvarea programelor modificate:
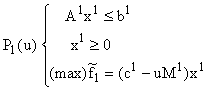
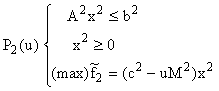
Agenții
comunică
autorității
centrale propunerile optimale ![]() și
și
![]() . În principiu,autoritatea centrala analizează
oportunitatea luării
în
considerare a acestor propuneri pentru maximizarea venitului pe economie și
poate decide modificarea sistemului de prețuri, mărind
prețurile
resurselor comune "intens" solicitate.
. În principiu,autoritatea centrala analizează
oportunitatea luării
în
considerare a acestor propuneri pentru maximizarea venitului pe economie și
poate decide modificarea sistemului de prețuri, mărind
prețurile
resurselor comune "intens" solicitate.
Noile prețuri sunt comunicate agenților; aceștia vor căuta noi soluții care să le maximizeze veniturile nete "corectate". Evident, prin creșterea prețurilor la anumite resurse comune, cererile "excesive" din aceste resurse vor fi "temperate". Formal, cele spuse înseamnă reluarea programelor P1(u), P2(u) cu u modificat!
Important este că într-un număr finit
de asemenea "dialoguri º schimburi de informații" între agenți și autoritatea centrală, vor rezulta soluțiile ![]() și
și ![]() care maximizează venitul total pe economie. În general,
care maximizează venitul total pe economie. În general, ![]() și
și ![]() nu coincid
cu una sau alta dintre propunerile agenților ( propuneri făcute în cadrul dialogului sus amintit) ci sunt combinații convexe ale acestora. Tot odată va rezulta și un sistem u* de prețuri pe resursele comune în raport cu care
nu coincid
cu una sau alta dintre propunerile agenților ( propuneri făcute în cadrul dialogului sus amintit) ci sunt combinații convexe ale acestora. Tot odată va rezulta și un sistem u* de prețuri pe resursele comune în raport cu care ![]() și
și ![]() maximizează veniturile nete individuale ale agenților! Spuunem că tripletul (
maximizează veniturile nete individuale ale agenților! Spuunem că tripletul (![]() ,
,![]() ,u*)
reprezintă
un echilibru pentru economia (liniară) considerată.
,u*)
reprezintă
un echilibru pentru economia (liniară) considerată.
Dialogul
dintre autoritatea centrală și agenți poate fi reprezentat astfel:
Nivel 2
Propuneri de
programe
de activitate

Nivel 1
Figura 4.1
Comparând această schemă cu cea din figura 3.4 se constată că cele spuse mai sus constituie o interpretare economică a principiului de descompunere Dantzig - Wolfe.
§5. Algoritmul de
descompunere Dantzig - Wolfe
În această secțiune vom arăta cum se rezolvă efectiv programul principal (PM) din secțiunea 3.
Să admitem pentru moment că am cunoaște toate constantele programului (PM). Vom
aplica acestui program versiunea revizuită a algoritmului simplex.
Să presupunem cunoscută o bază admisibilă B; în raport cu această bază partiționăm vectorul l al variabilelor:
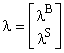
unde lB este vectorul variabilelor bazice iar lS al celor nebazice.
Soluția
![]() asociată bazei B va avea forma:
asociată bazei B va avea forma:
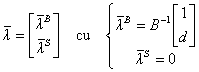
B fiind presupusă
admisibilă,
![]() . Fie:
. Fie:
![]()
vectorul multiplicatorilor simplex asociați bazei B (gB este vectorul format din coeficienții gk ai variabilelor bazice lk din lB)
Valoarea funcției obiectiv f în soluția de bază ![]() este:
este:
![]()
Elementele
numerice B-1,![]() și p sunt
reunite în
următorul
tabel simplex redus:
și p sunt
reunite în
următorul
tabel simplex redus:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lB |
|
|
B-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
p |
|
|
Tabelul 5.1
Din necesități care vor deveni evidente imediat, partiționăm p astfel: p = (p0,u)
p0 fiind prima componentă din p iar u reunind pe celelalte.
Testarea optimalității
soluției
![]() necesită
calcularea costurilor reduse:
necesită
calcularea costurilor reduse:
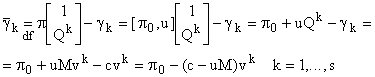
După
cum este bine știut,
dacă ![]() atunci
atunci ![]() este o soluție optimă a programului (PM). Pentru a vedea dacă se întâmplă acest lucru evaluăm:
este o soluție optimă a programului (PM). Pentru a vedea dacă se întâmplă acest lucru evaluăm:
![]()
Se observă
că
![]() este valoarea maximă a funcției
liniare
este valoarea maximă a funcției
liniare ![]() pe vârfurile
mulțimii
poliedrale mărginite
A .
pe vârfurile
mulțimii
poliedrale mărginite
A .
Conform teoremei centrale a programării liniare [9] , evaluarea acestui maxim nu necesită cunoaștera apriorică a vârfurilor v1,...,vs; este suficient să se rezolve programul liniar:
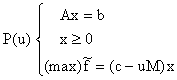
Fie v*
o soluție
optimă
a programului P(u) și ![]() valoarea funcției
obiectiv
valoarea funcției
obiectiv ![]() în
v*. v* este unul din vârfurile
mulțimii
A și putem scrie:
în
v*. v* este unul din vârfurile
mulțimii
A și putem scrie:
![]()
astfel că:
![]()
Dacă ![]() ( în fapt
( în fapt ![]() !) atunci
soluția
!) atunci
soluția
![]() este optimă.
este optimă.
Dacă ![]() se calculează Q*
= Mv* ,
se calculează Q*
= Mv* , ![]() și se introduce în baza curentă coloana
și se introduce în baza curentă coloana ![]() .
.
După
evaluarea coloanei ![]() se determină coloana care părăsește baza actuală și se pivotează tabelul simplex redus curent, intrându-se într-o nouă iterație.
se determină coloana care părăsește baza actuală și se pivotează tabelul simplex redus curent, intrându-se într-o nouă iterație.
Din descrierea făcută rezultă clar că ameliorarea soluției admisibile de bază ![]() - presupusă dată - nu a necesitat cunoașterea de la început a tuturor vârfurilor mulțimii
A ; vârful necesar în procesul de optimizare s-a obținut rezolvând un program liniar de forma P(u) cu un
vector u adecvat.
- presupusă dată - nu a necesitat cunoașterea de la început a tuturor vârfurilor mulțimii
A ; vârful necesar în procesul de optimizare s-a obținut rezolvând un program liniar de forma P(u) cu un
vector u adecvat.
În ceeace privește obținerea unei soluții de bază inițiale ![]() pentru programul (PM), aceasta se poate obține în maniera uzuală. Se pleacă de la o bază unitară ale cărei
coloane corespund:
pentru programul (PM), aceasta se poate obține în maniera uzuală. Se pleacă de la o bază unitară ale cărei
coloane corespund:
· (unele) unor (eventuale) variabile de abatere existente în blocul Mx = d;
·
(altele)
unor variabile artificiale introduse
în
anumite ecuații
ale blocului Mx = d și/sau în ecuația de convexitate ![]() .
.
În cazul în care au fost efectiv folosite variabile
artificiale, într-o
primă
fază
se va minimiza suma w a acestora. Coloanele care vor intra în bază se vor genera după schema generală de mai sus, funcția f fiind înlocuită cu funcția w care se minimizează!!
Exemplu 5.1 Se
consideră o
economie liniară
descentralizată
cu doi agenți,
fiecare oprând
câte
o activitate. Fie x1 și x2 nivelele de operare ale celor două activități. Resursele specifice controlate de către cei doi agenți limitează nivelele activităților după cum urmează:
x1 £ 4
, x2 £ 3
Susținerea
activităților necesită două resurse comune R1 și R2 al căror disponibil este limitat și controlat de o "autoritate centrală". La un nivel de operare egal cu
unitatea, vectorii consumurilor din resursele R1 și R2 sunt: ![]() pentru prima activitate și
pentru prima activitate și ![]() pentru a doua. Vectorul cantităților disponibile din resursele R1
și
R2 este
pentru a doua. Vectorul cantităților disponibile din resursele R1
și
R2 este ![]() . În fine, veniturile unitare sunt de 7 u.m. (unități
monetare) în
prima activitate și
de 6 u.m. în a doua.
. În fine, veniturile unitare sunt de 7 u.m. (unități
monetare) în
prima activitate și
de 6 u.m. în a doua.
Fiecare agent caută să obțină un venit cât mai mare, dar ei nu dețin controlul asupra resurselor comune. Pe
de altă
parte, economia fiind descentralizată, autoritatea centrală nu poate impune agenților nivelele la care să opereze activitățile proprii.
Obiectivul urmărit este maximizarea venitului total pe
economie.
Formal, problema constă în rezolvarea programului liniar:
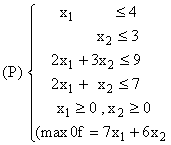
în situația încare nici agenții, nici autoritatea centrală nu dețin "informații complete" asupra programului (P).
După cum am văzut, rezolvarea este posibilă prin cooperarea
dintre agenți și autoritatea centrală, pe
baza algoritmului de descompunere Dantzig - Wolfe.
Partiționăm sistemul restricțiilor în două blocuri:
![]()
![]()
Principiul de descompunere propune rezolvarea programului:
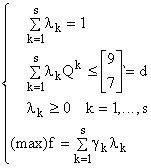
în care:
![]()
unde v1,...,vs sunt vârfurile mulțimii poliedrale:
A = 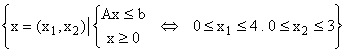
Este evidentă mărginirea mulțimii A .
O dată
obținută
soluția
optimă
![]() a programului propus,
soluția
optimă
a programului original (P) va rezulta din formula:
a programului propus,
soluția
optimă
a programului original (P) va rezulta din formula:
![]()
Aplicăm algoritmul simplex revizuit formei standard:
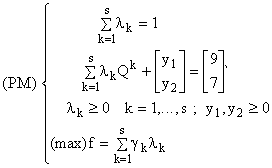
Variabilele de abatere y1 , y2 arată ce cantități din resursele comune R1 , R2
rămân nefolosite.
Programul (PM) are trei
restricții
și
se vede ușor
că
matricea sa conține
coloanele unitare ![]() și
și ![]() corespunzătoare variabilelor y1 , y2.
Pentru o bază
unitară
de start ne-ar trebui și
coloana
corespunzătoare variabilelor y1 , y2.
Pentru o bază
unitară
de start ne-ar trebui și
coloana ![]() care nu este tot așa de "vizibilă". Am putea introduce o variabilă artificială în restricția de convexitate
care nu este tot așa de "vizibilă". Am putea introduce o variabilă artificială în restricția de convexitate ![]() , dar putem
proceda, mai simplu, și astfel:
, dar putem
proceda, mai simplu, și astfel:
Se observă că vectorul nul ![]() este unul din vârfurile v1,...,vs
ale mulțimii
A (nu întotdeauna este așa!); putem presupune că v1 =
este unul din vârfurile v1,...,vs
ale mulțimii
A (nu întotdeauna este așa!); putem presupune că v1 =![]() .Atunci Q1
= Mv1 =
.Atunci Q1
= Mv1 = ![]() și
și ![]() .
.
În concluzie, matricea programului (PM) conține coloana unitară 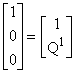 .
.
Astfel, pentru (PM)
dispunem de baza unitară corespunzătoare varibilelor l1, y1 și y2. Toate aceste variabile au
coeficienți
nuli în
funcția
obiectiv așa că :
![]() . În consecință,
vectorul multiplicatorilor simplex asociați bazei unitare
indicate este:
. În consecință,
vectorul multiplicatorilor simplex asociați bazei unitare
indicate este:
![]()
din care rezultă p0 = 0 , u = [0,0]. Vectorul valorilor variabilelor bazice are componentele:
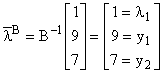
Valoarea funcției obiectiv este:
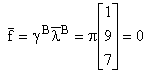
Toate aceste elemente formează tabelul simplex redus de start:
|
|
l1 |
1 |
1 |
0 |
0 |
|
(T1) |
y1 |
9 |
0 |
1 |
0 |
|
|
y2 |
7 |
0 |
0 |
1 |
|
|
f |
0 |
0 |
0 |
0 |
Tabelul 5.2
Considerarea vârfului v1 = ![]() sugerează că, la inițierea dialogului între
agenți și autoritatea centrală, se pleacă de la situația în care cele două
activități nu sunt operate: x1 = 0 , x2 = 0.
sugerează că, la inițierea dialogului între
agenți și autoritatea centrală, se pleacă de la situația în care cele două
activități nu sunt operate: x1 = 0 , x2 = 0.
y1 = 9 , y2 = 7 arată că resursele R1 și R2
nu sunt deocamdată solicitate.
Am văzut în secțiunea 4 că
vectorul u are semnificația de sistem de
prețuri pe resursele comune.Aceste prețuri sunt anunțate de către
autoritatea centrală agenților, care la rândul lor, își vor maximiza veniturile plătind pentru
resursele comune solicitate. Propunerile de programe de activitate sunt
comunicate de agenți autorității centrale. Aceasta preia propunerile și încearcă, pe baza lor și a
propunerilor mai vechi, să construiască o mixtură care să se încadreze în
disponibilul limitat de resurse comune și să conducă la un venit total cât mai
mare.
Iterația 1 Autoritatea centrală anunță sistemul de prețuri u = (0,0) , altfel spus oferă resursele
comune pe gratis.
Agenții rezolvă programul:
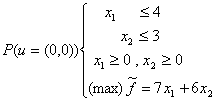
cu soluția optimă evidentă:
![]()
pe care o trimit ca propunere de program de activitate autorității centrale. Deoarece:
![]()
soluția din tabelul (T1) nu este optimă; baza curentă trebuie
schimbată prin introducerea unei noi coloane din matricea programului (PM).
Această coloană se generează astfel:
Vectorul 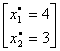 - notat în
teoria premergătoare cu v* - este un alt vârf al mulțimii A , să zicem v2. Calculăm:
- notat în
teoria premergătoare cu v* - este un alt vârf al mulțimii A , să zicem v2. Calculăm:
![]()
Coloana care
intră în bază va fi: 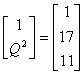 .
.
Calculele uzuale ale unei iterații din algoritmul simplex revizuit sunt
indicate mai jos

Tabelul 5.3
Iterația 2
Autoritatea centrală anunță noul sistem de prețuri: u = (46/17 , 0).
După cum se vede, resursa R2 este încă
oferită pe gratis, deoarece y2 = 20/17 arată că mixtura:
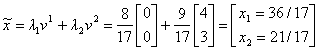
nu utilizează integral această resursă.
Calculăm vectorul veniturilor unitare nete:
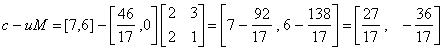
Agenții vor avea de rezolvat programul:
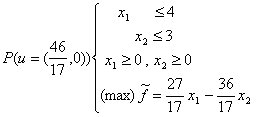
a cărui soluție optimă este:
![]()
( La prețurile actuale agentul 1 are un venit net pozitiv; el își poate permite să procure resursele R1 și R2 în cantitățile necesare pentru operarea activității sale la nivelul maxim posibil 4. Pentru agentul 2, resursa R1 este "prea scumpă": oricât de mic ar fi nivelul de operare al activității proprii, costul resurselor R1 și R2 depășește venitul său brut astfel că, pentru agentul 2, decizia va fi să nu facă nimic.)
Deoarece :
![]()
soluția din tabelul (T2) adică
mixtura ![]() descrisă mai sus, nu este optimă.
descrisă mai sus, nu este optimă.
Noua propunere a agenților 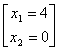 este un alt vârf, să zicem v3, al
mulțimii A , vârf care va produce
coloana ce îmbunătățește baza curentă:
este un alt vârf, să zicem v3, al
mulțimii A , vârf care va produce
coloana ce îmbunătățește baza curentă:
![]()
Intră în bază coloana:
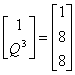
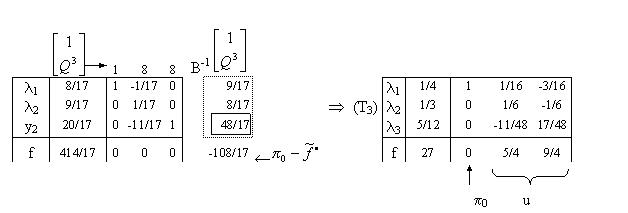
Pivotăm tabelul curent (T2):
Tabelul 5.4
Iterația 3
Noul sistem de prețuri pe resursele comune anunțat de autoritatea
centrală va fi:
u = (5/4 , 9/4)
Veniturile unitare nete ale agenților devin:
![]()
Astfel,
funcția obiectiv a programului P(u = (5/4 , 9/4)) este ![]() și în consecință
valoarea ei maximă va fi
și în consecință
valoarea ei maximă va fi ![]() . Deoarece
. Deoarece ![]() soluția din tabelul (T3) este
soluția optimă a programului (PM). Soluția optimă a programului original (P)
este mixtura convexă a celor trei propuneri v1,v2,v3:
soluția din tabelul (T3) este
soluția optimă a programului (PM). Soluția optimă a programului original (P)
este mixtura convexă a celor trei propuneri v1,v2,v3:
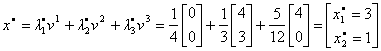
iar venitul maxim total are valoarea (max)f = 27.
§
6. Metoda generării
de coloane pentru problema croirii
După cum am văzut,
principiul de descompunere Dantzig - Wolfe rezolvă un program
liniar cu multe restricții
înlocuindu-l
cu un altul - numit program principal
- cu mai puține
restricții
dar cu foarte multe coloane (variabile)
care nu sunt disponibile de la început! În
orice fază
a rezolvării
programului principal, un număr relativ mic de coloane sunt cunoscute,
coloanele necesare îmbunătățirii
soluțiilor
intermediare fiind generate la "cerere".
Scopul acestei secțiuni
este acela de a arăta cum se aplică tehnica generării de coloane în
rezolvarea altor probleme de optimizare similare cum este de exemplu problema croirii introdusă
în
capitolul II, §2. În continuare vom vedea că
această
tehnică
necesită
luarea în
considerare a unei probleme de optimizare foarte simple ca structură
dar deosebit de importantă în optimizarea
combinatorială
- problema rucsacului. Pentru această
subproblemă,
în
secțiunea
următoare,
va fi prezentată
o metodă
specifică
de rezolvare bazată pe programarea
dinamică.
6.1 Problema croirii unidimensionale. Enunț
și
model matematic
Un număr
de m repere cu lungimile l1,l2,...,lm
trebuiesc croite din suporți
cu lungimea comună
L în cantitățile
b1,b2,...,bm
.Obiectivul constă
în
satisfacerea cererilor cu un consum minim
de suporți.
Presupunem că L și l1
,l2 ,..., lm
sunt exprimate prin
numere întregi
, pozitive și că L
> l1 >l2 >..>lm. Am
numit rețetă
de croire o modalitate de tăiere a unui suport în repere cu
lungimile cerute. Formal, o rețetă de croire se
identifică
cu un vector a = (a1,a2,...,am)
cu componente numere întregi nenegative în care ai reprezintă
numărul
reperelor cu lungimea li
rezultate din tăierea
suportului. Suma lungimilor reperelor astfel obținute nu depășește
lungimea suportului, astfel că:
![]()
Numărul
acestor rețete
este finit și ordonându-le
într-un
fel oarecare, de exemplu lexicografic,obținem
lista:
![]()
(pentru nevoi ulterioare rețetele vor fi scrise în coloană).
Dacă
notăm
cu xj numărul
de suporți
tăiați
după
rețeta
aj ( xj se mai numește și
multiplicitatea rețetei
aj) modelul matematic al
problemei de croire este:
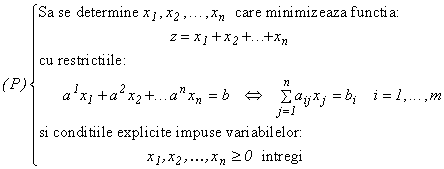
Deoarece pritre rețetele a1,a2,...,an
se numără
și
rețetele
unitare:
(1,0,0,...,0)
, (0,1,0,...,0) , ...,
(0,0,0,...,1)
problema (P) are soluții admisibile (cu componente) întregi
și
chiar soluție
optimă.
În cazul - frecvent întâlnit
în
practică
- în
care ne limităm
la utilizarea numai a așa numitelor rețete
maximale - adică a acelor rețete a = (a1,a2,...,am)
pentru care restul:
![]()
este mai mic decât
lungimea celui mai mic reper - problema de croire se formalizează
astfel:
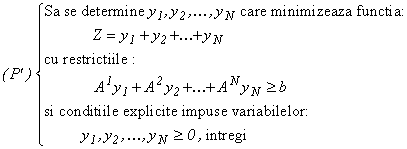
unde A1 , A2 ,
..., AN este (sub)lista
rețetelor
maximale, iar y1,y2,...,yN
sunt multiplicitățile
acestora.
Observație: Dacă în
modelul (P) toate restricțiile erau egalități
(aceasta însemnând
croirea reperelor "exact" în cantitățile
cerute) în
noul model (P') nu mai putem impune aceeași condiție
deoarece,prin restrângerea modalităților
de croire a unui suport, este posibil ca sistemul ![]() să
nu aibe soluții
întregi
nenegative! Iată
de ce, pentru a asigura compatibilitatea noului model suntem nevoiți
să
admitem că
anumite repere pot fi croite "în exces".
să
nu aibe soluții
întregi
nenegative! Iată
de ce, pentru a asigura compatibilitatea noului model suntem nevoiți
să
admitem că
anumite repere pot fi croite "în exces".
Programele întregi
(P) și
(P') sunt în
esență
echivalente în
sensul că
au același
optim întreg
iar soluția
optimă
a programului (P) utilizează cu prioritate rețete maximale; în
conssecință,
în
cele ce urmează
vom studia programul "mai general" (P).
Exemplul 6.1 Considerăm cazul croirii a trei repere cu lungimile l1 = 11, l2 =7 , l3
=4 din suporți
cu lungimea L = 19. În
următorul
tabel sunt indicate toate rețetele de croire și sunt puse în
evidență
rețetele
maximale.
|
Rețeta |
a1 º A1 |
a2 º A2 |
a3 |
a4 |
a5 º A3 |
a6 |
a7 º A4 |
a8 |
a9 |
a10 |
a11ºA5 |
a12 |
a13 |
a14 |
|
l1 = 11 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
l2 = 7 |
1 |
0 |
0 |
0 |
2 |
2 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
l3 = 4 |
0 |
2 |
1 |
0 |
1 |
0 |
3 |
2 |
1 |
0 |
4 |
3 |
2 |
1 |
|
Rest |
1 |
0 |
4 |
8 |
1 |
5 |
0 |
4 |
8 |
12 |
3 |
7 |
11 |
15 |
Tabelul 6.1
Pentru cererile b1 =12
, b2 =18 , b3 =30 :
· luarea în considerare a
tuturor rețetelor
de croire - maximale și nemaximale - conduce la modelul:
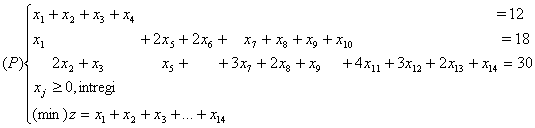
· având în
vedere numai rețetele
maximale obținem
modelul:
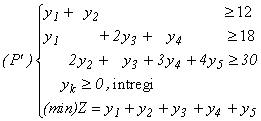
Ca orice problemă
de programare în
numere întregi
,(P) este foarte greu de rezolvat. În
marea majoritate a aplicațiilor practice vom fi fericiți
să
obținem
- în
timp util și
cu un efort computațional rezonabil - o soluție
"bună"
nu neapărat
optimală.
Așa
cum s-a indicat în
capitolul I,§1,o asemenea soluție s-ar putea obține rotunjind
convenabil soluția
optimă
a problemei relaxate (PL) dedusă
din (P) prin eliminarea cerinței
ca variabilele să
ia numai valori întregi.
Această
tactică
conduce la rezultate foarte bune în special în cazurile în
care cererile b1,b2,...,bm
sunt mari; într-adevăr
în
aceste cazuri, componentele soluției optime fracționare vor fi
suficient de mari astfel că pierderile datorate rotunjirii vor fi mici și
nesemnificative.
În continuare ne
vom ocupa de rezolvarea relaxatei (PL) a problemei de croire (P):
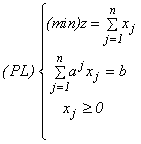
Dificultatea rezolvării acestei probleme rezidă
în
numărul
foarte mare de coloane (rețete) pe care le poate avea (mai cu seamă
în
situațile
reale) și
care - în
cazul rezolvării
"obișnuite"
- ar trebui mai întâi
generate. Vom vedea în continuare cum se poate evita acest
impediment.
6.2 Teoria metodei generării
de coloane
Vom aplica
problemei (PL) versiunea revizuită a algoritmului simplex.. La start, se poate
pleca cu baza formată din cele m rețete
unitare:
![]() cu tabelul redus:
cu tabelul redus:
|
e1 |
b1 |
1 |
|
|
|
|
e2 |
b2 |
|
1 |
|
|
|
M |
M |
|
|
O |
|
|
em |
bm |
|
|
|
1 |
|
f |
Sbi |
1 |
1 |
K |
1 |
Tabelul 6.2
Cel mai bine
este să se plece cu baza formată din cele m rețete unicat:
![]() în care:
în care:
![]() ,
, ![]() ,
,
,
, ![]()
și cu tabelul
simplex redus:
|
K1 |
b1/r1 |
1/r1 |
|
|
|
|
K2 |
b2/r2 |
|
1/r2 |
|
|
|
M |
M |
|
|
O |
|
|
Km |
bm/rm |
|
|
|
1/rm |
|
f |
Sbi/ri |
1/r1 |
1/r2 |
|
1/rm |
Tabelul 6.3
Fie B baza admisibilă curentă, 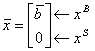 soluția asociată bazei
B. Presupunem disponibil tabelul simplex corespunzător; vezi tabelul 6.4
soluția asociată bazei
B. Presupunem disponibil tabelul simplex corespunzător; vezi tabelul 6.4
Reamintim că:
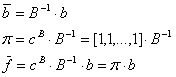
După cum se știe, soluția ![]() va fi optimă dacă, pentru toate coloanele
va fi optimă dacă, pentru toate coloanele ![]() avem:
avem:
![]()
Pentru a testa
îndeplinirea condiției de mai sus este suficient să calculăm:
![]()
și cum fiecare aj este
o soluție cu componente întregi nenegative a inecuației ![]() va fi suficient să
rezolvăm programul auxiliar:
va fi suficient să
rezolvăm programul auxiliar:
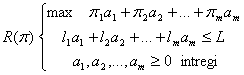
Dacă maximul funcției obiectiv din R(p) este £ 1 este clar că ![]() pentru toți j = 1,
,n și soluția
pentru toți j = 1,
,n și soluția ![]() asociată bazei B este
optimă.
asociată bazei B este
optimă.
Dacă maximul din R(p) este > 1 atunci soluția optimă a* a programului R(p) este o rețetă, fie ea ak , din lista ![]() a tuturor rețetelor,
cu proprietatea:
a tuturor rețetelor,
cu proprietatea:
![]() .
.
Introducem în baza curentă coloana ak
urmând instrucțiunile algoritmului simplex revzuit. Obținem o nouă bază
admisibilă B, o nouă soluție ![]() a problemei (PL) în general mai bună decât soluția veche
a problemei (PL) în general mai bună decât soluția veche ![]() și un nou tabel simplex
redus în care aopare un nou vector p de multiplicatori simplex.Pentru a testa
optimalitatea noii soliuții rezolvăm programul R(p) etc.
și un nou tabel simplex
redus în care aopare un nou vector p de multiplicatori simplex.Pentru a testa
optimalitatea noii soliuții rezolvăm programul R(p) etc.
Procesul iterativ se încheie într-un număr finit de pași cu găsirea soluției optime a problemei (PL).
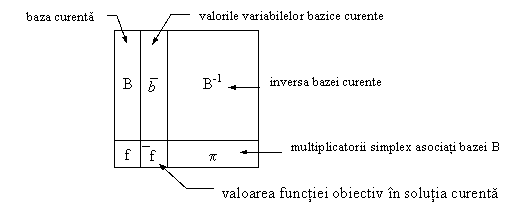
Tabelul 6.4
6.3
Rezumatul procedurii Generare de Coloane pentru rezolvarea relaxatei problemei de croire
Start Se pleacă cu baza formată din rețetele unicat(6.1) și cu tabelul simplex redus 6.3. Fie B baza
curentă și p = cBŚ B-1 vectorul multiplicatorilor simplex corespunzători.
Conținutul unei iterații:
Pasul
1 Se rezolvă problema auxiliară:
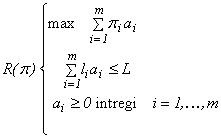
(vezi secțiunea
următoare
în
ceeace privește
modul algoritmic de rezolvare al problemei R(p) .
Pasul 2 Dacă maximul funcției obiectiv din R(p) este £ 1 stop:
soluția
curentă a
problemei (PL) este optimă. Altminteri:
Pasul 3 Fie a* soluția optimă a problemei R(p) . Se introduce în baza curentă B coloana a* (reindexată eventual cu numărul de ordine al iterației) urmând instrucțiunile algoritmului simplex revizuit. Se
revine la pasul 1 în cadrul unei noi iterații.
Exemplul 6.2 Vom rezolva relaxata (PL) a problemei de croire (P)
din exemplul 6.1 (sfătuim cititorul să ignore faptul că am generat deja toate rețetele de croire ale problemei...De altfel,
diferitele rețete
folosite de algoritm vor avea o notare diferită de cea din tabelul 6.1)
Start. Plecăm cu baza formată din rețetele unicat:
![]()
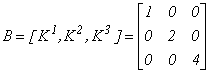 este o matrice diagonală a cărei inversă este :
este o matrice diagonală a cărei inversă este :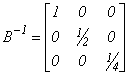 . Soluția
asociată
bazei B = [K1,
. Soluția
asociată
bazei B = [K1,
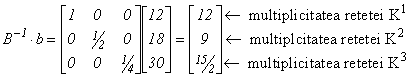
(celelalte rețete - pe cqre de fapt nu le știm - nu se folosesc).
Multiplicatorii
simplex asociați
bazei [K1,
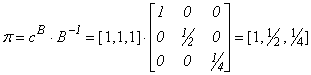
Valoarea funcției
obiectiv în
soluția
construită
este: `f =pŚb = 1Ś12 + ![]() Ś18 +
Ś18 + ![]() Ś30 = 28
Ś30 = 28![]() Ś
Ś
Tabelul simplex redus de start:
|
K1 |
12 |
1 |
0 |
0 |
|
|
9 |
0 |
1/2 |
0 |
|
K3 |
15/2 |
0 |
0 |
1/4 |
|
f |
57/2 |
1 |
1/2 |
1/4 |
Tabelul 6.5
Iterația 1 Se rezolvă problema :
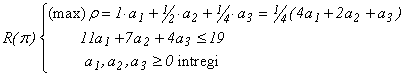
Prin simplă inspecție (în cazul de față) sau aplicând un algoritm adecvat dacă numărul reperelor este mare (vezi secțiunea următoare) se găsește (max)r = 3/2 > 1 și soluția optimă a* = (1,1,0) care este o rețetă maximală. Renotăm a* : A1 = (1,1,0)T și introducem A1 în baza curentă:
|
A1 |
ź |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
0 |
0 |
1 |
º pivot |
|
A1 |
12 |
1 |
0 |
0 |
|
|
|
9 |
0 |
1/2 |
0 |
1/2 |
|
Þ |
|
3 |
-1/2 |
1/2 |
0 |
|
|
K3 |
15/2 |
0 |
0 |
1/4 |
0 |
|
|
K3 |
15/2 |
0 |
0 |
1/4 |
|
|
f |
57/2 |
1 |
1/2 |
1/4 |
1/2 |
=(max)r-1 |
|
f |
45/2 |
1/2 |
1/2 |
1/4 |
|
Tabelul6.6a Tabelul 6.6b
Iterația 2 Rezolvăm problema:
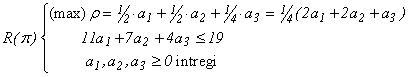
al cărei optim , (max)r = 5/4 > 1 , se atinge pe rețeta maximală a* = (0,2,1)T ,renotată A2. Introducem A2 în baza curentă:
|
A2 |
ź |
0 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
0 |
0 |
0 |
|
|
A1 |
12 |
1 |
0 |
0 |
|
|
|
3 |
-1/2 |
1/2 |
0 |
1 |
º pivot |
Þ |
A2 |
3 |
-1/2 |
1/2 |
0 |
|
|
K3 |
15/2 |
0 |
0 |
1/4 |
1/4 |
|
|
K3 |
27/4 |
1/8 |
-1/8 |
1/4 |
|
|
f |
45/2 |
1/2 |
1/2 |
1/4 |
1/4 |
=(max)r-1 |
|
f |
87/4 |
5/8 |
3/8 |
1/4 |
|
Tabelul6.7a Tabelul 6.7b
Iterația 3 Acum se rezolvă problema:
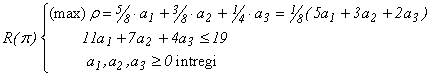
Se găsește (max)r = 9/8 > 1 și soluția optimă a* = (1,0,2)T ,renotată A3. Introducem A3 în baza curentă:
|
A3 |
ź |
1 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
0 |
0 |
1 |
|
|
A1 |
6/5 |
4/5 |
1/5 |
-2/5 |
|
|
A2 |
3 |
-1/2 |
1/2 |
0 |
-1/2 |
|
Þ |
A2 |
42/5 |
-2/5 |
2/5 |
1/5 |
|
|
|
27/4 |
1/8 |
-1/8 |
1/4 |
5/8 |
º pivot |
|
A3 |
54/5 |
1/5 |
-1/5 |
2/5 |
|
|
f |
87/8 |
5/8 |
3/8 |
1/4 |
1/8 |
=(max)r-1 |
|
f |
102/5 |
3/5 |
2/5 |
1/5 |
|
Tabelul6.8a Tabelul 6.8b
Iterația 4 Rezolvăm problema:
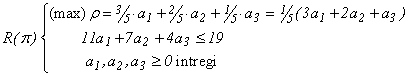
De această
dată
(max)r = 1 astfel că soluția curentă,înscrisă în tabelul 6. , este optimă.
În concluzie, soluția optimă fracționară a problemei de croire date utilizează:
· rețeta maximală A1 = (1,1,0)T cu
multiplicitatea ![]() ;
;
· rețeta maximală A2 = (0,2,1)T cu
multiplicitatea ![]() ;
;
· rețeta maximală A3 = (1,0,2)T cu
multiplicitatea ![]() .
.
Numărul
suporților
"consumați"
este : ![]() .
.
Observație: Reîntorcându-ne la problema de croire generală (P) și la relaxata acesteia se constată imediat că optimul întreg este cel puțin egal cu rotunjirea superioară a optimului fracționar!
În cazul de față rezultă că soluția optimă întreagă va utiliza cel puțin ![]() suporți.
suporți.
Să vedem acum cum se determină o soluție "bună" pentru problema de croire studiată.
Etapa 1 Se rotunjesc inferior multiplicitățile rețetelor din soluția optimă a problemei relaxate (PL):
![]()
Etapa 2 Se determină cantitățile de repere ce pot fi croite cu rețetele din soluția optimă fracționară dar cu multiplicitățile rotunjite inferior:
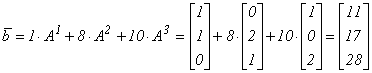
Etapa 3 Se determină cantitățile de repere care mai sunt de croit:
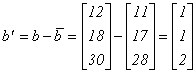
Etapa 4 Pentru "cererea reziduală" b' se aplică următoarea euristică, numită FFD (First Fit Decreasing):
· se determină prima rețetă în sens lexicografic care "încape" în b';
· se actualizează b' prin extragerea rețetei găsite și se reia pasul precedent.
În cazul nostru prima rețetă cuprinsă în b' este (1,1,0)T = A1.Actualizăm cererea reziduală:
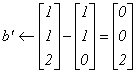
Au mai rămas
două
repere cu lungimea l3 = 4 a căror croire necesită consumarea unui suport .
Recapitulând, o soluție "bună" pentru croirea cantităților de repere cerute ar fi următoarea:
· se folosește rețeta A1 = (1,1,0) de 1 + 1 = 2
ori;
· se folosește rețeta A2 = (0,2,1) de 8 ori;
· se folosește rețeta A3 = (1,0,2) de 10 ori;
· se mai taie dintr-un suport două repere cu lungimea l3 = 4 adică se folosește reța nemaximală (0,0,2) .
În total se consumă 2 + 8 + 10 + 1 =21 suporți și în baza unei observații anterioare soluția construită este chiar optimă!
Concluzii finale
1. În soluția optimă a problemei relaxate se utilizează numai rețete maximale;
2. După aplicarea euristicii FFD asupra cererii
reziduale, pot apare și câteva rețete nemaximale - de regulă una singură;
3. Numeroasele experimente numerice au arătat că optimul întreg al problemei de croire
unidimensionale este de regulă egal cu rotunjirea întreagă superioară a optimului fracționar și numai în rare cazuri este mai mare decât aceasta cu exact o unitate!
§7 Programare dinamică
În această secțiune ne vom opri asupra problemei :
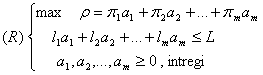
în care ![]() sunt întregi
pozitivi.
sunt întregi
pozitivi.
În secțiunea precedentă, (R) a apărut ca subproblemă în rezolvarea relaxatei problemei de croire
unidimensionale prin metoda generaării
de coloane. Este clar că eficacitatea metodei amintite depinde de
performanțele algoritmilor utilizați pentru rezolvarea problemei (R).
(R) este un progam liniar în numere întregi foarte
simplu, având o singură restricție.
În literatura de specialitate este cunoscută sub numele de problema rucsacului datorită următoarei interpretări:
ai este numărul pieselor de echipament de greutate li și utilitate pi
care trebuie luate într-o excursie într- un rucsac ce suportă o greutate
maximă L. Întrebare: ce piese de echipament trebuie alese și în câte exemplare
vor fi acestea introduse în rucsac astfel încât utilitatea încărcăturii să fie
maximă?
Firește, (R) poate fi rezolvată prin metodele specifice programării în numere întregi (plane de secțiune, Branch & Bound etc). Faptul că (R) are o singură restricție permite abordarea ei prin programare dinamică. Mai precis, pentru fiecare k = 1, ,m și fiecare întreg l =0,1, ,L considerăm problema:
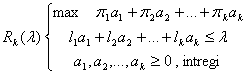
al cărei optim îl notăm cu rk(l). Este clar că R = Rm(l) și căaximul funcției obiectiv din R este rm(L).
Observăm că, pentru k fixat rk este o funcție de o singură variabilă ale cărei valori admisibile sunt 0,1, ,L.
Funcțiile r1 , r2 , , rm-1 , rm pot fi determinate astfel:
·
![]() =
=![]() l = 0,1,
,L (7.1)
l = 0,1,
,L (7.1)
·
pentru
k > 1 avem formula de recurență:
![]() ê
ê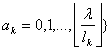 (7.2)
(7.2)
·
pentru
k = m este suficient să găsim numai valoarea funcției rm în L:
![]() ê
ê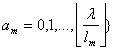
Relația (7.2)
arată că funcțiile r2,
,rm-1,rm
rezultă din niște procese de optimizare unidimensionale.
Să presupunem cunoscute funcțiile r1 , r2 ,
, rm-1 și valoarea rm(L) și să notăm cu ![]() valoarea variabilei ak care pentru l dat realizează maximul din formula de recurență (7.2). Pentru k =
1 avem
valoarea variabilei ak care pentru l dat realizează maximul din formula de recurență (7.2). Pentru k =
1 avem 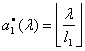 . Atunci, o soluție optimă a problemei (R) se găsește astfel:
. Atunci, o soluție optimă a problemei (R) se găsește astfel:
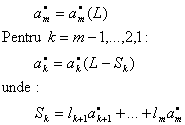
Observații: 1) În termenii problemei rucsacului rk(l) este valoarea maximă a unei încărcări a rucsacului ce nu depășește în greutate plafonul l și care este formată numai din primele k tipuri de echipament.
2) Prin programarea dinamică rezolvarea problemei
de optimizare multidimensională (R) este înlocuită cu o secvență de optimizări unidimensionale bazate pe formula de
recurență (7.2).
3) Ecuația funcțională (7.2), prin care funcțiile r1 , r2 ,
, rm-1 , rm se deduc una
din alta formalizează în cazul problemei (R) principiul central al programării dinamice datorat lui R. BELLMAN :
O strategie (secvențială) optimă are proprietatea că oricare ar fi
starea inițială și decizia inițială, deciziile rămase constituie o strategie
optimă în raport cu starea care rezultă din prima decizie.
Demonstrația formulei
(7.2)
Fie ![]() o valoare întreagă ,
o valoare întreagă , 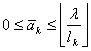 , dată variabilei ak
. Fie
, dată variabilei ak
. Fie ![]() o soluție optimă a problemei
o soluție optimă a problemei ![]() . Prin urmare:
. Prin urmare:
![]()
![]()
Deoarece 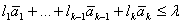 rezultă că
rezultă că 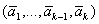 este o
soluție admisibilă a problemei
este o
soluție admisibilă a problemei 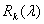 care dă funcției obiectiv valoarea:
care dă funcției obiectiv valoarea:
![]()
În consecință:
![]()
și cum ![]() a fost arbitrar aleasă (între 0 și
a fost arbitrar aleasă (între 0 și ![]() ) urmează
că:
) urmează
că:
![]() ê
ê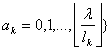
Pe de altă parte fie ![]() o soluție
optimă a problemei
o soluție
optimă a problemei ![]() .Prin urmare:
.Prin urmare:
![]()
![]()
Din ![]() rezultă
că
rezultă
că
![]() este o soluție admisibilă a problemei
este o soluție admisibilă a problemei ![]() și
deci:
și
deci:
![]()
Să
arătăm
că
în
ultima relație
avem egalitate. Presupunând prin absurd contrariul fie ![]() o soluție
optimă
a problemei
o soluție
optimă
a problemei ![]() . În consecință
vom avea:
. În consecință
vom avea:
![]()
![]()
![]()
Prin urmare ![]() este o soluție admisibilă a problemei
este o soluție admisibilă a problemei ![]() și
deoarece
și
deoarece
![]()
tragem concluzia
că
![]() nu este soluție
optimă
a problemei
nu este soluție
optimă
a problemei ![]() contrar ipotezei.
contrar ipotezei.
În definitiv:
![]()
astfel că:
![]()
![]() ê
ê 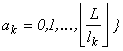
Egalitatea (7.2) este demonstrată.
Exemplul 7.1 Vom aplica procedura descrisă problemei:
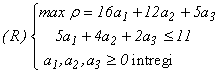
Iterația 1 Determinăm valorile funcției 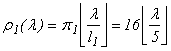 pentru l = 0,1,...,11
pentru l = 0,1,...,11
Ele sunt înscrise în tabelul 7.1
|
l |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
r1(l) |
0 |
0 |
0 |
0 |
0 |
16 |
16 |
16 |
16 |
16 |
32 |
32 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
Tabelul 7.1
Iterația 2 În
continuare calculăm valorile funcției
![]() ê
ê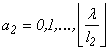 }=
}=
![]() ê
ê![]() } unde l = 0,1,...,11
} unde l = 0,1,...,11
Astfel, pentru l = 0,1,2,3 r2(l) = r1(l) ; pentru l = 4,5,6,7 vom avea:
![]() ê
ê![]() }=
}=![]()
iar pentru l =8,9,10,11
![]() ê
ê![]() }=
}=![]()
Rezultatele sunt afișate în tabelul 7.2
|
l |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
r2(l) |
0 |
0 |
0 |
0 |
12 |
16 |
16 |
16 |
24 |
28 |
32 |
32 |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
2 |
1 |
0 |
0 |
Tabelul 7.2
Iterația 3 În final vom evalua numai:
![]() ê
ê![]() =
=
![]()
![]()
Determinarea soluției optime ("de la sfârșit către început")
Pasul 1 ![]() ;
;
Pasul
2 ![]() ;
;
Pasul 3 ![]()
![]() .
.
Soluția
optimă a
problemei date este: ![]()
§ 8. Întrebări și
probleme
1.Este cunoscut
faptul că
problemele practice de optimizare de dimensiuni "mari" au o structură "specială". Ce înseamnă această structură specială în programarea liniară?
2.Ce
caracteristici are programul principal (Pm) rezultat din aplicarea
metodei de descompunere Dantzig - Wolfe? Ce metodă se utilizează pentru rezolvarea lui?
3.Se consideră un program liniar în formă canonică de maximizare a cărui mulțime de restricții a fost partiționată în două blocuri:
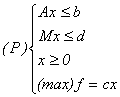 în notațiile
matriciale ale secțiunii 3.
în notațiile
matriciale ale secțiunii 3.
Să
presupunem că ![]() și
și ![]() sunt doi
vectori nenegativi de dimensiuni convenabile astfel încât:
sunt doi
vectori nenegativi de dimensiuni convenabile astfel încât:
·
![]() este soluția optimă a programului
este soluția optimă a programului
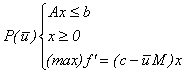
·
![]()
·
![]()
Să
se arate că ![]() este soluția optimă a programului (P).
este soluția optimă a programului (P).
.4. [3] Utilizați algoritmul de descompunere Dantzig - Wolfe la
rezolvarea următoarelor
programe liniare custructură bloc - diagonală și restricții de cuplare:
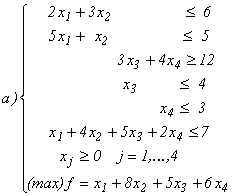
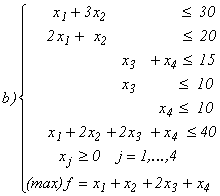
În rezolvarea subproblemelor de la nivelul
1 se poate folosi metoda grafică.
5. Pentru instalația de apă a unui imobil în construcție sunt necesare 80 de țevi de 2m, 40 de țevi de 2,50m și 30 de țevi cu lungimea de 3,50m. Aceste bucăți se taie din țevi cu lungimea de 9m.
a) Alcătuiți lista rețetelor maximale de croire;
b) Scrieți un program liniar în numere întregi pentru minimizarea numărului de țevi de 9m ce vor fi tăiate;
c) Rezolvați programul relaxat prin metoda generării de coloane;
d) Plecând de la soluția optimă fracționară construiți o soluție "bună" a problemei date;ar putea fi optimă soluția construită de dvs.?
6.Problema
rucsacului. Formulare și model matematic.Descrieți algoritmul de ezolvare al problemei
rucsacului prin programare dinamică.
7. Rezolvați problemele de tip rucsac:
![]()
![]()