ELEMENTE DE TEORIA GRAFURILOR

1. Noţiuni generale

În general, pentru situaţiile care necesită la rezolvare un oarecare efort mintal (şi un caz tipic este cel al celor din economie), se caută, în primul rând, o metodă de reprezentare a lor care să permită receptarea întregii probleme dintr-o privire (pe cât posibil) şi prin care să se evidenţieze cât mai clar toate aspectele acesteia.

În acest scop se folosesc imagini grafice gen diagrame, schiţe, grafice etc. O reprezentare dintre cele mai utilizate este cea prin grafuri. Acestea sunt utilizate în special pentru vizualizarea sistemelor şi situaţiilor complexe. În general, vom reprezenta componentele acestora prin puncte în plan iar relaţiile (legăturile, dependenţele, influenţele etc) dintre componente prin arce de curbă cu extremităţile în punctele corespunzătoare. Între două puncte pot exista unul sau mai multe segmente (în funcţie de câte relaţii dintre acestea, care ne interesează, există) iar segmentelor li se pot asocia sau nu orientări (după cum se influenţează cele două componente între ele), numere care să exprime intensitatea relaţiilor dintre componente etc.

Este evident, totuşi, că această metodă are limite, atât din punct de vedere uman (prea multe puncte şi segmente vor face desenul atât de complicat încât se va pierde chiar scopul pentru care a fost creat – claritatea şi simplitatea reprezentării, aceasta devenind neinteligibilă) cât şi din punct de vedere al tehnicii de calcul (un calculator nu poate "privi" un desen ca un om).

Din acest motiv, alături de expunerea naiv-intuitivă a ceea ce este un graf, dată mai sus, se impune atât o definiţie riguroasă cât şi alte modalităţi de reprezentare a acestora, adecvate în general rezolvărilor matematice.

Definiţia 1 Se numeşte multigraf un triplet G = (X, A, f) în care X şi A sunt două mulţimi iar f este o funcţie, definită pe produsul vectorial al lui X cu el însuşi (X² = X´X), care ia valori în mulţimea părţilor mulţimii A (notată P(A))

Mulţimea X se numeşte mulţimea nodurilor multigrafului şi elementele sale se numesc noduri (sau vârfuri) ale multigrafului, iar A reprezintă mulţimea relaţiilor (legăturilor) posibile între două noduri ale multigrafului.

Definiţia 2 Se numeşte graf orientat un multigraf în care mulţimea A are un singur element: A = {a}.

În acest caz mulţimea părţilor mulţimii A are doar două elemente: mulţimea vidă Æ şi întreaga mulţime A. Dacă unei perechi orientate (x_i, x_j) din X² i se asociază prin funcţia f mulţimea A atunci spunem ca există arc de la nodul x_i la nodul x_j iar perechea (x_i,x_j) se va numi arcul (x_i,x_j). Nodul x_i se numeşte nod iniţial sau extremitate iniţială a arcului (x_i,x_j) iar nodul x_j se numeşte nod final sau extremitate finală a arcului (x_i,x_j). Arcul (x_i,x_j) este incident spre interior vârfului x_j şi incident spre exterior vârfului x_i. Dacă pentru un arc nodul iniţial coincide cu nodul final atunci acesta se numeşte buclă. Nodurile x_i şi x_j se vor numi adiacente dacă există cel puţin unul din arcele (x_i,x_j) şi (x_j,x_i).

Dacă unei perechi orientate (x_i, x_j) din X² i se asociază prin funcţia f mulţimea vidă Æ atunci spunem că nu există arc de la nodul x_i la nodul x_j.

Este evident că a cunoaşte un graf orientat este echivalent cu a cunoaşte vârfurile şi arcele sale. Din acest motiv putem defini un graf orientat prin perechea (X,U), unde X este mulţimea vârfurilor sale iar U mulţimea arcelor sale.

De asemenea, putem cunoaşte un graf orientat cunoscând mulţimea nodurilor şi, pentru fiecare nod, mulţimea arcelor incidente spre exterior. Din acest motiv putem defini un graf orientat ca o pereche (X,G) unde X este perechea nodurilor iar G este o funcţie definită pe X cu valori în mulţimea părţilor lui X, valoarea acesteia într-un nod x_i, G(x_i) Í X fiind mulţimea nodurilor adiacente nodului x_i, prin arce pentru care x_i este extremitatea iniţială.

Definiţia 3 Se numeşte graf neorientat un multigraf în care mulţimea A are un singur element iar funcţia f are proprietatea:

f[(x_i,x_j)] = f[(x_j,x_i)] , oricare ar fi nodurile x_i şi x_j din X

În aceste condiţii, dacă f[(x_i,x_j)] = f[(x_j,x_i)] = A atunci perechea neorientată {x_i,x_j} este o muchie iar dacă f[(x_i,x_j)] = f[(x_j,x_i)] = Æ spunem că nu există muchie între vârfurile x_i şi x_j.

Deoarece, în cele mai multe din cazurile practice care vor fi analizate în acest capitol, situaţia este modelată matematic printr-un graf orientat, vom folosi, pentru simplificarea expunerii, denumirea de graf în locul celei de graf orientat iar în cazul în care graful este neorientat vom specifica acest fapt la momentul respectiv.

2. Moduri de reprezentare ale unui graf

A. O primă modalitate de reprezentare este listarea efectivă a tuturor nodurilor şi a arcelor sale.

B. Putem reprezenta graful dând pentru fiecare nod mulţimea nodurilor cu care formează arce în care el este pe prima poziţie.

C. Putem reprezenta geometric graful, printr-un desen în plan, reprezentând fiecare nod printr-un punct(cerculeţ) şi fiecare arc printr-un segment de curbă care are ca extremităţi nodurile arcului şi pe care este trecută o săgeată orientată de la nodul iniţial spre cel final.

D. Putem folosi o reprezentare geometrică în care nodurile sunt reprezentate de două ori, în două şiruri paralele, de la fiecare nod din unul din şiruri plecând săgeţi spre nodurile cu care formează arce în care el este pe prima poziţie, de pe al doilea şir (reprezentarea prin corespondenţă).

E. Un graf poate fi reprezentat printr-o matrice pătratică booleană, de dimensiune egală cu numărul de noduri, în care o poziţie a_ij va fi 1 dacă există arcul (x_i,x_j) şi 0 în caz contrar, numită matricea adiacenţelor directe.

F. Un graf poate fi reprezentat printr-o matrice pătratică latină, de dimensiune egală cu numărul de noduri, în care pe o poziţie a_ij va fi x_ix_j dacă există arcul (x_i,x_j) şi 0 în caz contrar.

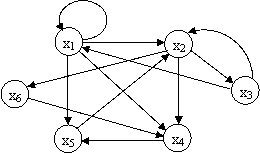
Exemplu: Dacă în reprezentarea A avem graful G = (X,U), unde X = {x₁, x₂, x₃, x₄, x₅, x₆} şi U = {(x₁,x₁), (x₁,x₂), (x₁,x₄), (x₁,x₅), (x₂,x₃), (x₂,x₄), (x₂,x₆), (x₃,x₁), (x₃,x₂), (x₄,x₅), (x₅,x₂), (x₆,x₄)}, atunci în celelalte reprezentări vom avea:

B x₁ ® {x₁, x₂, x₄, x₅} C

x₂ ® {x₃, x₄, x₆}

x₃ ® {x₁, x₂}

x₄ ® {x₅}

x₅ ® {x₂}

x₆ ® {x₄}

D (reprezentarea prin corespondenţă)

x₁ x₂ x₃ x₄ x₅ x₆

x₁ x₂ x₃ x₄ x₅ x₆

	x1	x2	x3	x4	x5	x6
x1	x1x1	x1x2	0	x1x4	x1x5	0
x2	0	0	x2x3	x2x4	0	x2x6
x3	x3x1	x3x2	0	0	0	0
x4	0	0	0	0	x4x5	0
x5	0	x5x2	0	0	0	0
x6	0	0	0	x6x4	0	0

	x1	x2	x3	x4	x5	x6
x1	1	1	0	1	1	0
x2	0	0	1	1	0	1
x3	1	1	0	0	0	0
x4	0	0	0	0	1	0
x5	0	1	0	0	0	0
x6	0	0	0	1	0	0

E F

3. Concepte de bază în teoria grafurilor

1. semigraf interior al unui nod x_k: este mulţimea arcelor = {(x_j,x_k)/ (x_j,x_k) Î U} care sunt incidente spre interior nodului x_k;

2. semigraf exterior al unui nod x_k: este mulţimea arcelor = {(x_k,x_i)/ (x_k,x_i) Î U} care sunt incidente spre exterior nodului x_k;

3. semigradul interior al unui nod x_k: este numărul arcelor care sunt incidente spre interior nodului x_k = cardinalul lui şi se notează cu ;

4. semigradul exterior al unui nod x_k: este numărul arcelor care sunt incidente spre exterior nodului x_k = cardinalul lui şi se notează cu ;

5. gradul unui nod x_k: este suma semigradelor nodului x_k: = + ;

6. nod izolat: este un nod cu gradul 0;

7. nod suspendat: este un nod cu gradul 1;

8. arce adiacente: arce care au o extremitate comună;

9. drum într-un graf: o mulţime ordonată de noduri ale grafului: (x₁, x₂, ..., x_k), cu proprietatea că există în graf toate arcele de forma (x_i,x_i+1) i = 1,...,k-1;

10. lungimea unui drum: este numărul arcelor care îl formează;

11. drum elementar: un drum în care fiecare nod apare o singură dată;

12. drum simplu: un drum în care fiecare arc apare o singură dată;

13. putere de atingere a unui nod x_i Î X în graful G: numărul de noduri la care se poate ajunge din x_i. Puterea de atingere se notează cu p(x_i), 1 £ i £ n şi evident p(x_i) ³ .

14. drum hamiltonian: un drum elementar care trece prin toate nodurile grafului;

15. drum eulerian: un drum simplu care conţine toate arcele grafului;

16. lanţ: un drum în care arcele nu au neapărat acelaşi sens de parcurgere;

17. circuit: un drum în care nodul iniţial coincide cu cel final;

18. circuit elementar: un drum în care fiecare nod apare o singură dată, cu excepţia celui final, care coincide cu cel iniţial;

19. circuit simplu: un drum în care fiecare arc apare o singură dată;

20. circuit hamiltonian: un circuit care trece prin toate nodurile grafului;

21. ciclu: este un circuit în care arcele nu au neapărat acelaşi sens de parcurgere;

22. ciclu elementar: un ciclu în care fiecare nod apare o singură dată, cu excepţia celui final, care coincide cu cel iniţial;

23. ciclu simplu: un ciclu în care fiecare arc apare o singură dată;

Observaţie: Într-un graf neorientat noţiunile de drum şi lanţ sunt echivalente şi de asemenea cele de circuit şi ciclu.

24. graf parţial al unui graf G = (X,U): este un graf G'(X,U') cu U' Ì U;

25. subgraf al unui graf G = (X,G): este un graf G'(X',G') unde X' Ì X şi G'(x_i) = G(x_i) Ç X' pentru orice x_i Î X';

26. graf redus al unui graf G = (X,U): este un graf G^*(X^*,U^*) unde X^* este formată din mulţimile unei partiţii de mulţimi nevide ale lui X, iar (,) există doar dacă i ¹ j şi există cel puţin un arc în U, de la un nod din la un nod din .

27. graf tare conex: este un graf în care între oricare două noduri există cel puţin un drum;

28. graf simplu conex: este un graf în care între oricare două noduri există cel puţin un lanţ;

Observaţie: Pentru grafuri neorientat noţiunile de tare conex şi simplu conex sunt echivalente, graful numindu-se doar conex;

29. componentă tare conexă a unui graf G = (X,U): este un subgraf al lui G care este tare conex şi nu este subgraful nici unui alt subgraf tare conex al lui G (altfel spus, între oricare două noduri din componentă există cel puţin un drum şi nu mai există nici un nod în afara componentei legat printr-un drum de un nod al componentei).

4. Găsirea drumurilor într-un graf orientat

Dacă privim graful ca imagine a unui sistem, nodurile reprezentând componentele sistemului, atunci o interpretare imediată a unui arc (x_i,x_j) este că, componenta x_i influenţează direct componenta x_j. Dacă nodurile au semnificaţia de stări posibile ale unui sistem atunci un arc (x_i,x_j) semnifică faptul că sistemul poate trece direct din starea x_i în starea x_j. În ambele cazuri se vede că avem de-a face doar cu informaţii despre legături directe; totuşi, chiar dacă o componentă x_i nu influenţează direct componenta x_j ea o poate influenţa prin intermediul altor componente, existând un şir de componente intermediare: x₁ x₂ ,..., x_k, fiecare influenţând-o direct pe următoarea şi x_i direct pe x₁ iar x_k direct pe x_j. Astfel, dacă dintr-o stare x_i nu se poate trece direct într-o stare x_j s-ar putea totuşi în mai multe etape, prin alte stări intermediare. Deoarece găsirea acestor influenţe sau treceri posibile este de obicei foarte importantă iar pentru un sistem cu mii sau zeci de mii de componente acest lucru nu mai poate fi făcut "din ochi", este necesară formalizarea noţiunii de "influenţe" şi "treceri" posibile, nu neapărat directe. Acest lucru a şi fost făcut mai sus, deoarece este evident că "x_i influenţează x_j" sau "din starea x_i se poate trece în starea x_j" este echivalent cu existenţa în graf a unui drum de la nodul x_i la nodul x_j.

În continuare vom da un algoritm prin care putem găsi toate drumurile dintr-un graf orientat cu un număr finit de noduri.

Pasul 1. Se construieşte matricea booleană a adiacenţelor directe corespunzătoare grafului, notată cu A. În aceasta se află, evident, toate drumurile de lungime 1.

Este interesant de văzut ce legătură există între această matrice şi drumurile de lungime 2. Fie două noduri x_i şi x_j oarecare din graf. Existenţa unui drum de lungime 2 între ele presupune existenţa unui nod x_k, din graf, cu proprietatea că există atât arcul (x_i,x_k) cât şi arcul (x_i,x_k). Pentru a vedea dacă acesta există, luăm pe rând fiecare nod al grafului şi verificăm dacă există sau nu ambele arce ((x_i,x_k) şi (x_i,x_k)). Aceasta este echivalent cu a verifica dacă, în matricea booleană a adiacenţelor directe, există vreun indice k astfel încât elementul k al liniei i şi elementul k al coloanei j să fie ambele egale cu 1. Dacă folosim operaţiile algebrei booleene de adunare şi înmulţire:

	0	1		0	1
0	0	1	0	0	0
1	1	1	1	0	1

atunci verificările de mai sus sunt echivalente cu a verifica dacă elementul de pe poziţia (i,j) din A² este egal cu 1. Valoarea 1 spune doar că există cel puţin un drum de lungime 2 de la x_i la x_j. Dacă dorim să vedem şi câte sunt, vom folosi regulile de înmulţire şi adunare obişnuită.

De asemenea, se poate observa că existenţa unui drum de lungime 3 de la x_i la x_j presupune existenţa unui nod x_k astfel încât să existe un drum de lungime 2 de la x_i la x_k şi un arc de la x_k la x_j, care este echivalent cu a verifica dacă există vreun indice k astfel încât elementul k al liniei i din matricea A² şi elementul k al coloanei j din A sunt ambele egale cu 1 sau, mai simplu, dacă elementul (i,j) din A³ este 1.

Din cele de mai sus se observă că existenţa drumurilor de lungime k este dată de valorile matricei A^k, dacă s-au folosit regulile algebrei booleene şi numărul lor este dat de A^k, dacă s-au folosit regulile obişnuite.

Pasul 2. Vom calcula succesiv puterile lui A până la puterea A^n-1

Dacă între nodurile x_i şi x_j există un drum de lungime ³ n atunci el va conţine un număr de noduri mai mare sau egal nu n+1 şi, cum în graf sunt doar n vârfuri, este clar că cel puţin unul, să zicem x_k, va apărea de două ori. Vom avea în acest caz un drum de la x_i până la prima apariţie a lui x_k, şi un drum de la ultima apariţie a lui x_k la x_j. Eliminând toate nodurile dintre prima apariţie a lui x_k şi ultima apariţie a sa vom obţine un drum de la x_i la x_j, în care x_k apare o singură dată. Aplicând acest procedeu pentru toate nodurile care apar de mai multe ori pe drum, vom obţine un drum de la x_i la x_j, în care fiecare nod apare o singură dată (deci un drum elementar), care are evident cel mult n-1 arce. În concluzie, dacă există vreun drum de la x_i la x_j atunci există şi un drum elementar şi, deci, va exista o putere a lui A, între A¹ şi A^n-1, în care poziţia (i,j) este diferită de 0. Pentru deciderea existenţei unui drum între oricare două noduri este suficientă, deci, calcularea doar a primelor n-1 puteri ale lui A.

Pasul 3. Se calculează matricea D = A + A² + ... + A^n-1

Dacă ne interesează doar existenţa drumurilor dintre noduri, nu şi numărul lor, vom folosi înmulţirea şi adunarea booleană şi conform observaţiei de mai sus:

d_ij =

În acest caz, observând că:

A×(A + I)^n–2 = ×A +×A² + ×A³ + ... + ×A^n–1 = A + A² + A³ + ... + A^n-1 = D

rezultă că e suficient să calculăm doar puterea n-2 a matricei A + I şi apoi s-o înmulţim cu A. Avantajul acestei metode, în ceea ce priveşte economia de timp, este susţinut şi de următoarea observaţie: dacă D conţine toate perechile de arce între care există drum atunci:

D = (A + A² + ... + A^n-1) + Aⁿ + Aⁿ⁺¹ + ... + A^n+k = D oricare ar fi k ³ 0 Þ

Þ A×(A + I)^n–2+k = (A + A² + ... + A^n-1) + Aⁿ + Aⁿ⁺¹ + ... + A^n+k-1 = D = A×(A + I)^n–2 Û

ÛA×(A + I)^n–2+k = A×(A + I)^n–2 oricare ar fi k ³ 0

deci de la puterea k = n-2 toate matricile A^k sunt egale. Putem, deci, calcula direct orice putere a lui A+I mai mare sau egală cu n-1 (de exemplu calculând (A+I)², (A+I)⁴, (A+I)⁸, ..., , r fiind prima putere a lui 2 pentru care 2^r ³ n-2).

Procedeul de mai sus nu asigură decât aflarea faptului dacă există sau nu drum între două noduri, eventual ce lungime are şi câte sunt de această lungime. Totuşi, în problemele practice cel mai important este să ştim care sunt efectiv aceste drumuri. Deoarece toate drumurile pot fi descompuse în drumuri elementare şi în problemele practice în general acestea sunt cele care interesează, paşii următori ai algoritmului vor fi dedicaţi găsirii lor. Pentru găsirea acestora se foloseşte reprezentarea grafului prin matricea latină de la cazul F.

Pasul 4. Construim matricea latină L asociată grafului, unde:

l_ij =

şi matricea , definită prin:

=

numită matricea latină redusă.

Găsirea unui drum de lungime 2 de la x_i la x_j presupune găsirea unui nod cu proprietatea că există arcele (x_i,x_k) şi (x_k,x_j) şi memorarea vectorului (x_i, x_k, x_j). Aceasta este echivalent cu a găsi un indice k astfel încât elementul de pe poziţia k a liniei i, din matricea L, să fie x_i,x_k şi elementul de pe poziţia k al coloanei j, din matricea , să fie x_j. Vom înmulţi deci matricea L cu matricea , folosind însă nişte reguli de calcul speciale, numite înmulţire şi adunare latină.

Definiţia 1: Se numeşte alfabet o mulţime de semne numite simboluri sau litere {s_i/iÎI} unde I este o mulţime oarecare de indici, finită sau nu.

Definiţia 2: Se numeşte cuvânt un şir finit de simboluri notat .

Definiţia 3: Se numeşte înmulţire latină o operaţie definită pe mulţimea cuvintelor unui alfabet, notată "", astfel:

=

(produsul a două cuvinte se obţine prin concatenarea lor)

Înmulţirea latină este asociativă, are ca element neutru cuvântul vid, nu e comutativă şi un element este inversabil doar dacă este cuvântul vid.

Definiţia 3: Se numeşte adunare latină o funcţie definită pe mulţimea cuvintelor unui alfabet cu valori în mulţimea parţilor mulţimi cuvintelor, notată "" astfel:

=

(suma a două cuvinte este mulţimea formată din cele două cuvinte)

Pasul 5. Se calculează succesiv matricile:

L² = L , L³ = L² , ... ,L^k+1 = L^k

folosind operaţiile de înmulţire şi adunare latină, alfabetul fiind mulţimea nodurilor grafului, unde operaţia de înmulţire este uşor modificată, produsul dintre două elemente ale matricilor fiind 0, dacă unul dintre ele este 0 sau au un nod comun şi este produsul latin al lor, în caz contrar.

Din felul cum a fost construită, matricea L^k va conţine toate drumurile elementare de lungime k. Cum un drum elementar poate avea cel mult n noduri (câte are graful cu totul) rezultă că:

- primele n-1 puteri ale lui L conţin toate drumurile elementare din graf;

- puterile lui L mai mari sau egale cu n au toate elementele egale cu 0;

- matricea L^n-1 conţine toate drumurile hamiltoniene din graf (dacă există).

Observaţie: Deoarece obţinerea matricii D prin metoda de mai sus presupune un volum foarte mare de calcule (de exemplu, dacă graful are 100 de noduri, ridicarea unei matrici de 100×100 la puterea 100) pentru obţinerea acesteia se poate aplica şi următorul algoritm:

Pas 1. Se construieşte matricea de adiacenţă A;

Pas 2. Pentru fiecare linie i se adună boolean la aceasta toate liniile j pentru care a_ij = 1.

Pas 3. Se reia pasul 2 până când, după o aplicare a acestuia, matricea rămâne aceeaşi (nu mai apare nici un 1)

Ultima matrice obţinută este matricea drumurilor D numită şi matricea conexiunilor totale.

Această metodă, deşi mai simplă nu spune însă şi care sunt aceste drumuri, pentru găsirea lor aplicându-se, de exemplu, înmulţirea latină

5. ARBORI. Problema arborelui de valoare optimă

În acest subcapitol grafurile vor fi considerate neorientate.

5.1. Noţiunea de arbore

Un arbore este un graf neorientat, finit, conex şi fără cicluri. Grafurile din fig. 4.1. sunt arbori.

Studiul arborilor este justificat de existenţa în practică a unui număr mare de probleme care pot fi modelate prin arbori. Dintre acestea amintim:

1. construirea unor reţele de aprovizionare cu apă potabilă (sau cu energie electrică sau termică etc) a unor puncte de consum, de la un punct central;

2. construirea unor căi de acces între mai multe puncte izolate;

3. desfăşurarea unui joc strategic;

4. luarea deciziilor în mai multe etape (arbori decizionali);

5. evoluţii posibile ale unui sistem pornind de la o stare iniţială;

6. construirea unei reţele telefonice radiale, a unei reţele de relee electrice;

7. legarea într-o reţea a unui număr mare de calculatoare;

8. organigramele întreprinderilor;

9. studiul circuitelor electrice în electrotehnică (grafe de fluenţă etc);

10. schemele bloc ale programelor pentru calculatoare etc.

În toate problemele de mai sus se doreşte ca, dintre muchiile unui graf neorientat, să se extragă arborele optim din mulţimea tuturor arborilor care pot fi extraşi din graful dat.

Deoarece definiţia arborelui este dificil de aplicat pentru deciderea faptului că un graf este arbore sau nu (şi în special sunt greu de verificat conexitatea şi mai ales existenţa ciclurilor) există mai multe caracterizări posibile ale unui arbore, acestea fiind date de teorema de mai jos:

Teoremă. Dacă H este un graf neorientat finit, atunci următoarele afirmaţii sunt echivalente:

1) H este arbore;

2) H nu conţine cicluri şi, dacă se unesc printr-o muchie două noduri neadiacente, se formează un ciclu (şi numai unul). Arborele este, deci, pentru o mulţime de noduri dată, graful cu numărul maxim de arce astfel încât să se păstreze proprietatea că nu are cicluri);

3) H este conex şi dacă i se suprimă o muchie se creează două componente conexe (arborele este graful conex cu numărul minim de arce);

4) H este conex şi are n-1 muchii;

5) H este fără cicluri şi are n-1 muchii;

6) Orice pereche de noduri este legată printr-un lanţ şi numai unul.

Demonstraţie :

1)Þ 2). între cele două noduri adiacente noii muchii introduse exista deja un drum în fostul graf. Acest drum, împreună cu noul arc va forma evident un ciclu şi afirmaţia 2) a fost demonstrată.

2)Þ3). Pentru oricare două vârfuri neunite printr-o muchie, adăugând muchia dintre cele două vârfuri s-ar crea, conform ipotezei, un ciclu care conţine această muchie, deci două drumuri între cele două noduri, din care unul nu conţine noua muchie, adică în graful iniţial exista un drum între cele două noduri. Dacă nu există cicluri înseamnă că între oricare două noduri există un singur drum. Pentru două noduri unite printr-o muchie, aceasta este chiar drumul corespunzător celor două noduri. Dacă suprimăm această muchie între cele două noduri nu va mai exista nici un drum, formându-se două componente conexe.

3)Þ4). Demonstraţia se face prin inducţie după n = numărul de noduri ale grafului. Pentru n=2 este evident. Presupunem afirmaţia adevărată pentru toate grafurile cu cel mult n noduri. Dacă graful are n+1 noduri, prin suprimarea unei muchii se formează două componente conexe fiecare având cel mult n noduri (n₁ £ n, n₂ £ n şi n₁ + n₂ = n+1) şi deci au n₁ – 1 respectiv n₂ – 1 muchii. În concluzie graful iniţial a avut (n₁ – 1) + (n₂ – 1) +1 = n₁ + n₂ – 1= (n+1)-1 muchii, ceea ce era de demonstrat.

4)Þ5). Dacă ar avea un ciclu atunci prin suprimarea unui arc al acestuia ar rămâne de asemenea conex. Eliminăm acest arc apoi repetăm procedeul pentru graful parţial rămas şi tot aşa până când nu mai rămâne nici un ciclu. În acest moment graful rămas este conex şi nu are cicluri deci este arbore şi deci are n-1 arce, în contradicţie cu faptul că el avea n-1 arce înainte de a începe suprimarea arcelor;

5)Þ6). Dacă între două noduri ar exista două drumuri atunci acestea ar forma la un loc un ciclu. Deci între 2 noduri este cel mult un drum. Dacă între două noduri nu ar exista nici un drum ar fi cel puţin două componente conexe în graf, fiecare fiind arbore (pentru că nu există cicluri) şi deci fiecare ar avea un număr de arce cu 1 mai mic decât numărul de noduri. Făcând adunarea, ar rezulta că în graf sunt strict mai puţin de n-1 arce.

6)Þ1). Dacă H ar avea un ciclu, între două noduri ale acestuia ar exista două lanţuri, în contradicţie cu ipoteza.

Presupunem că avem un graf pentru care am verificat deja dacă este conex. Dacă nu este atunci acesta, evident, nu are nici un graf parţial care să fie arbore.

Presupunem de asemenea că fiecărei muchii îi este asociată o valoare reală.

5.2. Algoritmi pentru găsirea arborelui de valoare optimă

Vom da mai jos trei algoritmi pentru determinarea unui graf parţial al grafului, care să fie arbore şi pentru care suma valorilor arcelor sale să fie minimă (sau maximă).

Toţi algoritmii descrişi în continuare extrag arborele prin colectarea una câte una a muchiilor acestuia.

A. Algoritmul lui Kruskal

Pasul 1. Dintre toate muchiile grafului se alege muchia de valoare minimă (maximă). Dacă minimul este multiplu se alege la întâmplare una din muchiile respective. Deoarece acest "la întâmplare" trebuie cumva tradus în limbajul calculatorului, în cazul implementării unui program bazat pe acest algoritm, vom perturba din start valorile muchiilor, la k muchii cu aceiaşi valoare V adunând respectiv valorile e, 2e, ... , ke, unde e este foarte mic (în orice caz, ke mai mic decât diferenţa dintre valoarea acestor arce si valoarea imediat superioară a unui arc), pozitiv.

Pasul 2. Dintre toate muchiile rămase, se alege cea de valoare minimă (maximă);

Pasul 3. Dintre toate muchiile rămase, se alege cea de valoare minimă (maximă), astfel încât să nu se formeze cicluri cu cele deja alese;

Pasul 4. Se reia algoritmul de la pasul 3 până se colectează n-1 muchii.

Deşi s-a demonstrat că algoritmul găseşte întotdeauna arborele optim, el are dezavantajul că este foarte laborios (de fiecare dată trebuie calculat minimul unei mulţimi mari sau foarte mari – există situaţii în practică în care graful are sute de mii de arce) şi, în plus, trebuie aplicat un algoritm special ca să respectăm condiţia de a nu se forma cicluri, la alegerea unui nou arc.

O metodă posibilă este ca, după adăugarea fiecărui arc, să se împartă graful în componente conexe şi să alegem apoi un arc care nu are ambele extremităţile în aceeaşi componentă conexă.

De asemenea este clar că, în cazul existenţei arcelor de valori egale, deoarece se alege la întâmplare, există mai multe variante de evoluţie a alegerii arcelor. Totuşi, cu toate că pot fi mai multe grafuri la care se poate ajunge prin acest algoritm, ele vor avea toate aceeaşi valoare (minima (sau maxima) posibilă).

B. Algoritmul lui Sollin

Pasul 1. Pentru fiecare nod se alege muchia adiacentă de valoare minimă (maximă).

Pasul 2. Se evidenţiază componentele conexe, existente în graful parţial format din arcele alese până în acest moment.

Pasul 3. Pentru fiecare componentă conexă se alege muchia adiacentă de valoare minimă (maximă). Prin muchie adiacentă unei componente conexe înţelegem o muchie care are o singură extremitate printre nodurile componentei respective.

Pasul 4. Se reia algoritmul de la pasul 2 până rămâne o singură componentă conexă. Aceasta este arborele optim căutat.

Acest algoritm asigură de asemenea găsirea arborelui optim, necesită mult mai puţine calcule (la fiecare alegere se calculează minimul doar pentru muchiile adiacente unui singur nod), evită automat formarea ciclurilor, dar, pentru grafuri foarte mari, la un moment dat pot exista atât de multe componente conexe care trebuie memorate succesiv, încât calculul devine greoi sau, pe calculator, depăşeşte posibilităţile de memorare ale calculatorului.

C. O variantă a algoritmului lui Kruskal

Pasul 1. Dintre toate muchiile grafului se alege cea de valoare minimă (maximă);

Pasul 2. Dintre toate muchiile adiacente componentei conexe formată din arcele alese până în acest moment, se alege cea de valoare minimă (maximă);

Pasul 3. Se reia pasul 2 până se colecţionează n-1 muchii.

Algoritmul are toate avantajele algoritmului lui Sollin şi, în plus, lucrează cu o singură componentă conexă, fiind mult mai uşor de implementat pe calculator şi mult mai rapid în execuţie.

Exemplu: Administraţia unei localităţi montane a hotărât construirea unor linii de teleferic care să lege oraşul de cele 8 puncte turistice importante din jurul acestuia. În urma unui studiu au fost puse în evidenţa toate posibilităţile şi costurile de conectare a obiectivele turistice între ele şi cu oraşul, acestea fiind prezentate în figura 4.2.

Se cere găsirea variantei de construcţie de cost minim, care să asigure accesul din oraş la oricare din obiectivele turistice.

Rezolvare

Condiţia de cost minim implică două obiective:

1. Să se construiască minimul de arce necesare;

2. Să se construiască cele mai ieftine legături.

Referitor la numărul de arce necesar, facem observaţia că, dacă din oraş se va putea ajunge la orice obiectiv turistic, atunci se va putea ajunge şi de la orice staţiune la oricare alta (trecând prin oraş), deci trebuie ca arcele alese pentru construcţie să formeze la un loc un graf conex.

În concluzie, căutăm un graf parţial conex cu un număr minim de arce, adică un arbore. În plus, suma costurilor arcelor sale trebuie să fie minimă. Vom aplica pe rând cei trei algoritmi pentru găsirea acestuia:

A. Kruskal

La primul pas poate fi ales unul din arcele OP₃ sau OP₇, ele având valoarea minimă 2. Putem alege oricum primul arc dintre cele două pentru că la al doilea pas va fi ales celălalt.

La pasul trei poate fi ales unul din arcele OP₅, OP₆ sau P₁P₆ care au valoarea minimă 3. Nici în acest caz nu are vre-o importanţă ordinea alegerii, deoarece pot fi alese succesiv toate trei fără a se forma nici un ciclu.

Al şaselea arc poate fi ales dintre arcele P₄P₅ şi P₁P₂, care au valoarea minimă 4. Nici în acest caz nu are vre-o importanţă ordinea alegerii, deoarece pot fi alese succesiv ambele, fără a se forma nici un ciclu.

Următoarea valoare disponibilă a unui arc este 5, dar arcul opt nu poate fi ales dintre arcele OP₁, P₆P₇, deşi au valoarea minimă 5. Arcul OP₁ nu poate fi ales deoarece s-ar forma ciclul OP₁P₆, iar P₆P₇ ar duce la ciclul OP₆P₇. Următoarea valoare minimă este 6, pentru arcul P₅P₇ dar nu poate fi ales deoarece se formează ciclul OP₅P₇.

Valoarea următoare, 7, o au arcele OP₄, P₂P₃ şi P₅P₈. OP₄ nu poate fi ales deoarece s-ar forma ciclul OP₅P₄. Arcul P₂P₃ nu poate fi ales deoarece s-ar forma ciclul OP₆P₁P₂P₃. Arcul P₅P₈ nu formează nici un ciclu şi el va fi al optulea arc ales. În acest caz, deoarece s-au adunat 8 arce într-un graf cu 9 noduri, am obţinut graful căutat.

Acest arbore este reprezentat în figura 4.3.

B. Sollin

Vom alege:	pentru nodul O	®	arcul OP3
	pentru nodul P1	®	arcul P1P6
	pentru nodul P2	®	arcul P1P2
	pentru nodul P3	®	arcul OP3
	pentru nodul P4	®	arcul P4P5
	pentru nodul P5	®	arcul OP5
	pentru nodul P6	®	arcul P1P6
	pentru nodul P7	®	arcul OP7
	pentru nodul P8	®	arcul P5P8

Rezultă graful parţial:

După cum se vede, s-au format două componente conexe: C₁ = {P₁,P₂,P₆}

C₂ = {O,P₃,P₄,P₅,P₇,P₈}.

Vom alege: pentru C₁ ® arcul OP₆

pentru C₂ ® arcul OP₆

şi obţinem o singură componentă conexă, care este arborele căutat.

C. Varianta algoritmului lui Kruskal

Succesiunea alegerii arcelor va fi:

1	®	OP3
2	®	OP7
3	®	OP6
4	®	OP5
5	®	P1P6
6	®	P1P2
7	®	P4P5
8	®	P5P8

6. Cuplajul a două mulţimi disjuncte Probleme de afectare (de repartiţie)

În practica economică sunt foarte des întâlnite probleme în care se doreşte asocierea optimă a elementelor unei mulţimi X = {x₁, x₂, ... , x_n} cu elementele unei alte mulţimi Y = {y₁, y₂, ... , y_m} în condiţiile unor limitări existente (şi cunoscute) ale posibilităţilor de asociere.

În general, fiecare asociere posibilă x_i « y_j aduce un anumit efect a_ij (profit, cost etc) care poate fi calculat şi vom presupune că este cunoscut.

Limitările asupra asocierilor se traduc de obicei prin faptul că:

1. Un element x_i poate fi asociat doar cu anumite elemente din Y şi reciproc;

2. La sfârşit, fiecărui element din X i s-a asociat cel mult un element din Y şi reciproc.

Asocierea optimă presupune, de obicei, două obiective:

1. Să se facă maximul de asocieri;

2. Suma efectelor asocierilor să fie maximă (sau minimă, în funcţie de semnificaţia acestora).

Reprezentarea geometrică a situaţiei de mai sus este un graf de forma:

numit graf bipartit.

Definiţia 1: Se numeşte graf bipartit un graf G = (X, U) în care mulţimea nodurilor poate fi împărţită în două mulţimi disjuncte A şi B astfel încât orice arc are extremitatea iniţială în A şi cea finală în B.

Definiţia 2: Se numeşte cuplaj al unui graf bipartit o submulţime de arce W Í U cu proprietatea că nu există două arce adiacente (sau altfel spus, pentru orice nod există cel mult un arc incident acestuia).

Definiţia 3: Se numeşte cuplaj maxim un cuplaj cu proprietatea că orice arc care nu face parte din cuplaj este adiacent cu un arc din cuplaj ( Û orice arc am adăuga, nu mai rămâne cuplaj Û nu există nici un cuplaj în care să se includă strict Û conţine numărul maxim de arce neadiacente)

Este evident că numărul de arce ale unui cuplaj este mai mic sau egal cu numărul de elemente din fiecare din mulţimile A şi B (£ min (½A½,½B½). Este interesant de văzut însă cât de mare este el efectiv şi în ce condiţii este egal chiar cu min (½A½,½B½).

Referitor la prima întrebare, în 1931 König a demonstrat o teoremă care permite stabilirea numărului de arce ale unui cuplaj maxim:

Teoremă: Numărul maxim de arce ale unui cuplaj într-un graf bipartit G = (AÈB, G) este egal cu

În ceea ce priveşte a doua problemă, observăm mai întâi că putem presupune că întotdeauna ½A½£½B½, în caz contrar inversând sensul tuturor arcelor grafului, problema rămânând aceeaşi.

În acest caz:

= ½A½ Û – ½A½ = 0 Û = 0 Û

Û = 0 Û oricare ar fi C Í A

sau altfel spus, pentru orice submulţime C a lui A, mulţimea nodurilor atinse de arce care pleacă din nodurile sale, adică G(C), are cel puţin atâtea elemente cât C.

De exemplu, la repartizarea angajaţilor pe posturi, fiecare angajat poate obţine un post dorit dacă şi numai dacă oricare ar fi mulţimea de r angajaţi există cel puţin r posturi diferite din care pot alege.

Presupunem, în continuare, că s-a asociat fiecărui arc (x_i,x_j) o valoare v_ij.

Definiţia 4: Se numeşte valoare a unui cuplaj suma valorilor arcelor care îl formează.

În acest moment putem spune că determinarea unei asocieri optime a mulţimilor X şi Y de la început este echivalentă matematic cu determinarea unui cuplaj maxim de valoare optimă (minimă sau maximă) în graful bipartit asociat.

Dintre problemele întâlnite în practica economică, ce se reduc matematic la găsirea unui cuplaj maxim de valoare optimă, amintim:

1. Problema repartizării muncitorilor unei secţii la utilajele acesteia în funcţie de pregătirea şi preferinţele muncitorilor, complexitatea maşinilor etc;

2. transferarea unor informaţii într-un grup;

3. Repartizarea angajaţilor pe posturi;

4. Formarea grupelor de lucru după afinităţile dintre membrii colectivului.

În 1955, bazându-se pe teorema lui König, H.W. Kuhn a elaborat un algoritm, cunoscut în literatura de specialitate sub denumirea de algoritmul ungar, cu ajutorul căruia se poate determina un cuplaj maxim de valoare minimă într-un graf bipartit pentru care ½A½=½B½= n.

El se bazează pe observaţia că, dacă se adună (sau scade) aceeaşi număr la toate valorile arcelor, nu se modifică ierarhia cuplajelor maxime, în ceea ce priveşte valoarea lor.

Vom prezenta algoritmul concomitent cu rezolvarea unui caz particular, pentru o mai bună receptare a acestuia:

"Într-o secţie produsele finite se obţin în urma efectuării succesive a 6 operaţii pe 6 maşini. În această secţie sunt angajaţi 6 muncitori, fiecare fiind calificat pentru efectuarea oricărei din cele 6 operaţii. Pentru a optimiza activitatea în secţie cei 6 muncitori au fost supuşi la un test în care fiecare a prelucrat un număr de piese, pe toate cele şase maşini. În final, calculându-se timpul mediu în care muncitorul M_i efectuează operaţia O_j s-au obţinut valorile (în ore) date în tabelul de mai jos:

	M1	M2	M3	M4	M5	M6
O1	4	3	6	2	6	8
O2	5	4	8	3	8	9
O3	5	6	8	2	8	7
O4	4	5	7	2	7	8
O5	4	6	6	3	6	7
O6	6	6	8	3	8	9

Să se găsească acea repartiţie a muncitorilor la maşini astfel încât timpul în care o piesă se prelucrează succesiv pe cele 6 maşini să fie minim."

Pasul 1. Se construieşte matricea pătratică M care are elementele:

m_ij =

Pentru exemplul ales vom avea: M =

Pasul 2. Se scade din fiecare linie minimul acesteia apoi, în matricea obţinută, din fiecare coloană minimul acesteia (se poate face şi invers, rezultatul final va fi acelaşi). Pentru exemplul dat vom obţine succesiv matricile:

M₁ = şi apoi M₂ =

Ultima matrice este cea asupra căreia se aplică următoarele calcule. În acest moment pe fiecare linie şi pe fiecare coloană se află cel puţin un 0, care corespunde celui mai mic timp. Se încearcă în continuare folosirea doar a acestor repartizări:

Pasul 3. În ordinea crescătoare a numărului de zerouri şi de sus în jos (în cazul existenţei mai multor linii cu acelaşi număr de zerouri ) se încadrează pentru fiecare linie zeroul a cărui coloană conţine cele mai puţine zerouri (primul de la stânga dintre acestea, în caz de egaliate) şi se barează celelalte zerouri de pe linia şi coloana acestuia. Pe parcursul algoritmului sunt luate în considerare la numărare doar zerourile neîncadrate şi nebarate încă. În final, pe fiecare linie şi pe fiecare coloană va fi cel mult un zero încadrat. Dacă în final sunt n (= dimensiunea matricei) zerouri, atunci arcele corespunzătoare formează cuplajul căutat. Dacă sunt mai puţine se trece la pasul 4.

În exemplul nostru avem trei linii cu câte un zero (a 3-a, a 4-a şi a 5-a) .Îl încadrăm pe cel de pe linia 3 (prima dintre ele) şi barăm restul zerourilor de pe linia 3 şi coloana 3, obţinând:

În acest moment pe liniile 1 şi 2 se află un zero. Se încadrează cel de pe linia 1 şi se barează celelalte de pe linia 1 şi coloana 2, obţinând:

Ultima linie cu zerouri este linia 5 din care îl încadrăm pe primul şi le barăm pe celelalte:

În total nu sunt 6 zerouri încadrate (sunt doar trei) şi deci trecem la pasul 4.

Pasul 4. La acest pas se va stabili numărul minim posibil de linii şi coloane care să conţină toate zerourile matricii. În acest sens vom proceda astfel:

a) se marchează liniile care nu au nici un zero încadrat;

b) se marchează coloanele care au un zero barat pe o linie marcată;

c) se marchează liniile care au un zero încadrat pe o linie marcată (dacă există);

Se repetă operaţiile b) şi c) până nu mai poate fi marcată nici o linie şi nici o coloană.

În cazul nostru vom avea: a) ® se marchează liniile 2, 4 şi 6;

b) ® se marchează coloanele 2 şi 4;

c) ® se marchează liniile 1 şi 3;

b) ® nu mai marcăm nici o coloană deoarece nu mai există nici un zero barat pe liniile 1 şi 3, care să corespundă unei coloane nemarcate;

c) ® nu mai marcăm nici o linie, deoarece nu a mai apărut nici o coloană marcată.

Rezultă:

Pasul 5. Se taie liniile nemarcate şi coloanele marcate:

Pasul 6. Se împart elementele matricei în trei grupe:

G₁ = elemente aflate la intersecţii de linii netăiate cu coloane netăiate;

G₂ = elemente situate la intersecţii de linii tăiate cu coloane netăiate sau de linii netăiate cu coloane tăiate;

G₃ = elemente situate la intersecţii de coloane tăiate cu linii tăiate

Pasul 7. Se găseşte minimul grupei G₁, care se scade din fiecare element al lui G₁ şi se adună la fiecare element al grupei G₃. Elementele grupei G₂ rămân neschimbate.

Pentru exemplul dat, minimul lui G₁ este 1 şi obţinem noua matrice:

Pasul 8. Se reia algoritmul de la pasul 3.

Vom avea după marcare:

Deoarece avem 6 zerouri încadrate, am obţinut cuplajul maxim de valoare minimă căutat, căruia îi va corespunde repartizarea muncitorilor pe operaţii de mai jos:

care duce la o durată totală a prelucrării unei piese de 6 + 4 + 7 + 6 + 3 = 26 ore

Observaţie: Deoarece regula de a alege de sus în jos la linii cu acelaşi număr de zerouri este arbitrară şi de asemenea alegerea primului zero de la stânga, putem ajunge şi la alte cuplaje maxime, dar toate vor avea aceeaşi valoare, cea minimă. De exemplu, un alt cuplaj optim este:

adică

care are de asemenea valoarea 26.

Observaţia 1. Dacă dorim un cuplaj de valoare maximă atunci vom calcula la pasul 1 matricea M astfel:

1. Construind matricea A de elemente:

a_ij =

2. Matricea M va avea componentele: m_ij =

apoi aplicăm în continuare algoritmul.

Observaţia 2. Dacă ½A½¹½B½ atunci aplicăm acelaşi algoritm cu singura diferenţă că ne vom opri când vom obţine un număr de zerouri egal cu min (½A½,½B½).

7. Drumuri şi circuite hamiltoniene

Una dintre cele mai cunoscute probleme economice este problema comis voiajorului. Comis voiajorul este un individ care trebuie să prezinte s-au să distribuie marfa comandată la o serie de centre distribuite în general neliniar pe o anumită zonă teritorială (localităţile dintr-un judeţ, magazinele dintr-un cartier, persoanele dintr-un sat etc). Dacă numărul de obiective care trebuie vizitate este mare sau foarte mare iar timpul disponibil foarte limitat atunci devine vitală o asemenea organizare a trecerii pe la fiecare obiectiv încât să se efectueze în timpul minim posibil. Acest timp minim se traduce prin drumul cel mai scurt, iar cel mai scurt drum este evident cel în care se trece pe la fiecare obiectiv o singură dată. În plus, la sfârşit trebuie să se afle în punctul iniţial, adică sediul firmei la care lucrează.

O reprezentare a regiunii aprovizionate, în care centrele pe la care se trece sunt vizualizate prin puncte iar căile de acces la acestea prin segmente de curbe, va fi evident un graf, problema reducându-se la a găsi circuitul hamiltonian de lungime minimă.

În timp, s-au evidenţiat o multitudine de probleme reductibile la găsirea unui drum (sau circuit) hamiltonian într-un graf, cum ar fi:

1. Problema poştaşului (găsirea traseului cel mai scurt care trece pe la toate locuinţele ce aparţin de oficiul poştal la care lucrează acesta);

2. Problema adunării deşeurilor (cel mai scurt drum care trece pe la toate punctele de depozitate a deşeurilor);

3. Problema succesiunii operaţiilor (executarea mai multor operaţii pe o maşină în acea ordine în care suma timpilor consumaţi cu pregătirea maşinii pentru trecerea de la o operaţie la următoarea să fie minim)

4. Ordinea lipirii unor componente electronice pe o placă, etc;

Determinarea drumurilor hamiltoniene

Problema determinării drumului (circuitului) hamiltonian de valoare optimă s-a dovedit deosebit de dificilă, neexistând nici acum un algoritm care să rezolve problema în timp polinomial şi nici măcar o metodă simplă prin care să se decidă dacă într-un graf dat există sau nu drumuri hamiltoniene.

Există însă mai mulţi algoritmi, unii exacţi alţii heuristici, care reuşesc, într-un caz sau altul, să rezolve problema satisfăcător şi în timp util.

A. Algoritmul lui Foulkes

Pasul 1. Se scrie matricea booleană A asociată grafului G.

Pasul 2. Se determină matricea D a drumurilor grafului G prin procedeul expus la începutul capitolului şi apoi matricea M = I + D.

Pasul 3. Se împarte mulţimea nodurilor grafului în submulţimi disjuncte astfel:

1. Se consideră în matricea M liniile pline (cu toate elementele 1). Nodurile ce corespund liniilor pline cu 1 formează submulţimea C₁.

2. Se elimină liniile şi coloanele care corespund nodurilor din submulţimea stabilită.

3. Se reia raţionamentul de la punctul 1 pe matricea redusă obţinută la punctul 2 obţinându-se următoarea submulţime şi în continuare toate celelalte până se epuizează toate liniile matricei.

Pasul 4. Se construieşte graful G' în care:

1. Nodurile care formează o submulţime sunt reprezentate prin puncte în interiorul unui dreptunghi şi între acestea se trasează arcele existente în graful iniţial G.

2. Se trasează legăturile dintre submulţimi. Ele sunt reprezentate prin arcele existente în graful iniţial G între nodurile submulţimii C₁ şi cele ale submulţimii C₂, între nodurile submulţimii C₂ şi cele ale submulţimii C₃ etc.

Pasul 5. Se găsesc drumurile hamiltoniene

Un drum hamiltonian se găseşte plecând de la un vârf din submulţimea C₁, trecând prin toate vârfurile acesteia cu un drum hamiltonian, din ultimul vârf la care se ajunge în C₁ trecând la un vârf din C₂, parcurgând în continuare un drum hamiltonian în a doua submulţime şi tot aşa, trecând prin toate submulţimile şi parcurgând, deci, toate nodurile grafului iniţial, o singură dată. Aplicând acest procedeu în toate modurile posibile se obţin toate drumurile hamiltoniene din graful iniţial G. (Observaţie: poate să nu existe nici un drum hamiltonian în graful G, caz în care algoritmul se opreşte deoarece la un anumit pas nu mai exista nici o linie plina cu 1).

Observaţie. Algoritmul lui Foulkes reduce găsirea drumurilor hamiltoniene în graful iniţial G (care în problemele practice este foarte mare) la găsirea mai multor drumuri hamiltoniene mai mici în componente tare conexe ale grafului. Dacă un graf are o singură componentă tare conexă, algoritmul lui Foulkes nu este eficient, în acest caz trebuind aplicaţi alţi algoritmi cum ar fi cel bazat pe înmulţirea latină.

B. Algoritmul lui Chen pentru determinarea drumurilor hamiltoniene

în grafuri fără circuite

Fie G = (X,U) un graf orientat fără circuite, cu n noduri: X = {x₁, x₂, … , x_n}. Vom considera că am calculat matricea drumurilor D şi puterile de atingere ale tuturor nodurilor.

Dacă în graful G există un drum de la nodul x_i la nodul x_j atunci evident p(x_i) > p(x_j), deoarece în orice vârf în care se poate ajunge din x_j se poate ajunge şi din x_i dar din x_j nu se poate ajunge în x_j pentru că nu există circuite.

Teorema 2.3 (Chen) Un graf cu n noduri, fără circuite conţine un drum hamiltonian dacă şi numai dacă există relaţia:

Demonstraţie

“Þ” Fie H un drum hamiltonian şi presupunem că nodurile grafului au fost notate în ordinea în care apar în acest drum. Atunci din orice nod x_i se poate ajunge în toate nodurile cu indice mai mare şi numai în acestea (altfel ar exista circuite) şi deci puterea unui nod x_i este n – i, de unde:

= (n – 1) + (n – 2) + … + 1 + 0 =

“Ü” Ordonând vârfurile în ordinea descrescătoare a puterii lor de atingere (i > j Û p(x_i) < p(x_j)) şi cum graful nu are circuite, vom obţine o matrice D cu toate zerourile deasupra diagonalei (evident pe o poziţie (i,i) nu se află nici un 1 iar dacă ar fi un 1 pe poziţia (i,j) cu i > j ar însemna că din x_i se poate ajunge în x_j, deci în toate nodurile în care se poate ajunge din x_j, iar din x_j nu se poate ajunge în x_i, deci p(x_i) > p(x_j) în contradicţie cu ipoteza de ordonare a nodurilor). Cum deasupra diagonalei sunt poziţii iar suma puterilor vârfurilor este chiar rezultă că toate poziţiile de deasupra diagonalei sunt 1. Aceasta înseamnă că există toate arcele de forma (x_i,x_i+1) (altfel n-ar exista drum de la x_i la x_i+1, deoarece toate drumurile au indicii nodurilor în ordine descrescătoare) şi deci drumul hamiltonian (x₁, x₂, … , x_n) q.e.d.

Teorema 2.4 Dacă într-un graf orientat fără circuite există un drum hamiltonian atunci acesta este unic.

Demonstraţie Deoarece un drum hamiltonian se identifică cu o permutare a nodurilor grafului, existenţa a două drumuri hamiltoniene implică existenţa a două permutări distincte a nodurilor grafului şi cum două permutări distincte diferă prin cel puţin o inversiune vor exista două noduri x_i şi x_j în ordinea x_i ® x_j pe un drum şi invers pe celălalt, existând deci un drum atât de la x_i la x_j cât şi de la x_j la x_i, cele două formând împreună un circuit, în contradicţie cu ipoteza.

Pe aceste teoreme se bazează algoritmul lui Chen de determinare a drumului hamiltonian într-un graf orientat fără circuite:

Pasul1. Se scrie matricea de adiacenţă A

Pasul2. Se calculează matricea drumurilor D

Pasul3. Dacă există un indice i cu d_ii = 1 atunci graful are circuite, nu se poate aplica algoritmul lui Chen şi algoritmul se opreşte. Dacă nu, se trece la pasul 4.

Pasul4. Se calculează puterile de atingere pentru fiecare nod.

Pasul5. Dacă nu se verifică relaţia atunci graful nu are drumuri hamiltoniene şi algoritmul se opreşte, altfel se trece la pasul 6.

Pasul6. Se ordonează nodurile în ordinea descrescătoare a puterilor lor de atingere şi obţinem drumul hamiltonian căutat.

C. Algoritmul lui Kaufmann

Pasul 1. Construim matricea latină L asociată grafului, unde:

l_ij =

Pasul 2. Construim matricea , definită prin:

=

numită matricea latină redusă.

Pasul 3. Se calculează succesiv matricile:

L² = L, L³ = L², ..., L^k+1 = L^k, ...

folosind operaţiile de înmulţire şi adunare latină, alfabetul fiind mulţimea nodurilor grafului, unde operaţia de înmulţire este uşor modificată, produsul dintre două elemente ale matricilor fiind 0, dacă unul dintre ele este 0 sau au un nod comun, şi este produsul latin al lor, în caz contrar.

Din felul cum a fost construită, matricea L^k va conţine toate drumurile elementare de lungime k. Cum un drum elementar poate avea cel mult n noduri (câte are graful cu totul) rezultă că:

- primele n-1 puteri ale L conţin toate drumurile elementare din graf;

- puterile lui L mai mari sau egale cu n au toate elementele egale cu 0;

- matricea L^n-1 conţine toate drumurile hamiltoniene din graf.

Pasul 4. Dacă se doresc şi circuitele atunci se verifică pentru fiecare drum hamiltonian dacă poate fi completat până la un circuit (adică dacă există în graf arcul care uneşte nodul final cu cel iniţial);

Pasul 5. Dacă se doreşte şi drumul (sau circuitul) de valoare optimă (maximă sau minimă) se calculează suma valorilor pentru fiecare drum şi/sau circuit şi se alege cel cu valoarea optimă.

În concluzie, metoda înmulţirii latine (A. Kaufmann – J. Melgrange) determină toate drumurile elementare din graf, prin calcularea matricelor M⁽¹⁾, M⁽²⁾, M⁽³⁾, …, M^(n-1).

În matricea M^(n-1) se citesc drumurile hamiltoniene.

Această metodă a înmulţirii latine (algoritmul lui Kaufmann) este utilă, mai ales, în cazul grafurilor tare conexe, unde algoritmul lui Foulkes nu este eficient. Totuşi, metoda este greu de aplicat în grafuri cu un număr mare de noduri. În acest caz este preferabil să se construiască graful condensat, să se determine drumurile hamiltoniene în fiecare în parte cu algoritmul lui Kaufmann şi apoi, ca la algoritmul lui Foulkes, să se caute drumurile hamiltoniene în graful iniţial.

D. Un algoritm bazat pe algoritmul ungar

Fie G = (X,U) un graf orientat cu n noduri X = {x₁, x₂, … , x_n}.

Pasul 1. Se construieşte graful bipartit H = (AÈB,V) în care A = B = X şi V = U (adică am folosit pentru G reprezentarea prin corespondenţă).

Pasul 2. Se găseşte pentru graful H cuplajul maxim de valoare minimă.

Pasul 3. Se construieşte graful parţial al lui G format doar cu arcele cuplajului găsit. Este uşor de demonstrat că, componentele tare conexe ale acestuia sunt toate nişte circuite. Dacă s-a format un singur circuit acesta este circuitul hamiltonian de valoare minimă. Dacă s-au format mai multe se trece la pasul 4.

Pasul 4. Pentru fiecare arc aflat pe circuitul de lungime minimă (dacă sunt mai multe se iau în considerare arcele tuturor) se reia algoritmul de la pasul 1 pentru graful parţial rezultat din G prin eliminarea acestui arc.

Pasul 5. Pentru fiecare graf parţial se continuă procedeul până se ajunge la unul din cazurile:

Cazul1. Cuplajului maxim găsit îi corespunde un singur circuit. Dacă acest circuit este primul obţinut atunci valoarea sa i se atribuie unei variabile Z şi circuitul este păstrat. Dacă nu este primul atunci valoarea sa se compară cu Z şi, dacă este mai mică, ea devine noua valoare a lui Z şi circuitul se păstrează, eliminându-l pe cel corespunzător fostei valori a lui Z. În caz contrar se trece la alt graf parţial neanalizat încă.

Cazul2. Cuplajul maxim are o valoare mai mare decât Z. Pentru acest graf parţial se abandonează ramificarea.

Pasul 6. Se continuă analiza grafurilor parţiale până sunt analizate toate ramificaţiile. Valoarea Z finală este valoarea circuitului de valoare minimă iar circuitul corespunzător este cel optim.

Analiza de mai sus poate fi schematizată printr-un arbore de tipul:

în care fiecare nod este un graf parţial de analizat, iar pentru fiecare arc, nodul inferior este un graf parţial care provine din graful corespunzător nodului superior, prin suprimarea unui arc de pe circuitele de lungime minimă corespunzătoare cuplajului maxim de valoare minimă al acestuia.

Observaţie: Algoritmul asigură găsirea circuitului de valoare minimă iar în cazul în care algoritmul lui Foulkes nu funcţionează este o alternativă mai bună decât algoritmul lui Kaufmann. Totuşi el nu lucrează în timp polinomial şi în unele cazuri (de exemplu cazuri în care se formează foarte multe cicluri cu lungime minimă) necesită un număr imens de calcule.

În aceste cazuri se pot folosi metode euristice prin care se elimină din start o serie de arce, considerate a avea valori prea mari pentru a se putea afla pe circuitul hamiltonian de valoare minimă, apoi se aplică în graful parţial rămas unul din algoritmii de mai sus.

8. Drumuri optime într-un graf

În marea majoritate a problemelor care pot fi modelate prin grafuri nu ne interesează numai dacă există sau nu legături între componentele reprezentate prin nodurile grafului ci şi intensitatea acestora. Această intensitate are semnificaţia unei valori numerice (pozitive sau negative) asociate arcului corespunzător legăturii a cărei intensitate o măsoară.

În aplicaţiile economice această valoare poate fi:

- lungimea drumului dintre două localităţi;

- costul parcurgerii rutei reprezentate prin arcul corespunzător;

- durata parcurgerii rutei respective;

- cantitatea transportată pe ruta respectivă;

- capacitatea maximă a rutei respective;

- câştigul realizat prin trecerea de la o stare la alta a sistemului;

- consum de energie pentru efectuarea trecerii respective;

- punctaj realizat etc.

Una din problemele care poate apărea în aceste situaţii este găsirea, pentru o anumită pereche de noduri (sau mai multe perechi), a drumului optim între acestea.

Pentru formalizarea problemei vom introduce noţiunea de valoare a unui drum, care este egală cu suma valorilor arcelor care îl compun. Vom nota în continuare valoarea unui arc (x_i,x_j) cu v(x_i,x_j) sau cu v_ij. În aceste condiţii putem enunţa problema drumului optim astfel:

"Dat un graf G = (X,U) şi o funcţie care asociază fiecărui arc o valoare reală, să se găsească, pentru o pereche dată de noduri, drumul (drumurile) de valoare optimă (minimă sau/şi maximă) între cele două noduri şi valoarea acestuia (acestora)"

Deoarece este vorba de găsirea minimului unei mulţimi de numere reale, prima întrebare care se pune este dacă aceasta admite minim. Dacă mulţimea nodurilor grafului este infinită atunci pot exista o infinitate de drumuri elementare distincte între cele două noduri şi mulţimea valorilor acestora poate avea orice formă (închisă sau nu, mărginită sau nu) devenind foarte greu de caracterizat cazurile când minimul dorit există. Deoarece totuşi majoritatea covârşitoare a problemelor economice se modelează prin grafuri cu număr finit de noduri, ne vom limita în continuare doar la acestea.

Un număr finit de noduri n atrage după sine existenţa unui număr finit de arce (cel mult n²) şi a unui număr finit de drumuri elementare ( cel mult n×n!×). Deoarece oricărui drum d îi corespunde un drum elementar d_e (obţinut prin eliminarea tuturor subcircuitelor lui d) putem calcula valoarea oricărui drum ca sumă între valoarea drumului elementar corespunzător şi valorile unor subcircuite ale sale, fiecare înmulţită cu numărul de parcurgeri ale circuitului respectiv.

În concluzie, dacă există un circuit de valoare negativă înseamnă că există drumuri de valoare oricât de mică (cele care conţin acest circuit), obţinută prin parcurgerea acestuia de oricâte ori dorim) şi, deci, mulţimea valorilor drumurilor este nemărginită inferior, neexistând drum de valoare minimă. Dacă există un circuit de valoare pozitivă atunci există drumuri de valoare oricât de mare şi mulţimea valorilor drumurilor este nemărginită superior, neexistând drum de valoare maximă.

Dacă nu există circuite de valoare negativă atunci valoarea oricărui drum este mai mare sau egală cu a drumului elementar corespunzător, deci drumul de valoare minimă (dacă există) va fi un drum elementar. Cum mulţimea drumurilor elementare este finită (şi deci şi mulţimea valorilor lor) va avea minorant şi am lămurit problema compatibilităţii problemei. Analog, dacă nu există circuite de valoare pozitivă atunci valoarea oricărui drum este mai mică sau egală cu a drumului elementar corespunzător, deci drumul de valoare maximă (dacă există) va fi un drum elementar. Cum mulţimea drumurilor elementare este finită (şi deci şi mulţimea valorilor lor), va avea majorant.

Obs. 1. Dacă în graf nu există decât arce de valoare pozitivă atunci există drum de valoare minimă.

Obs. 1. Dacă în graf nu există decât arce de valoare negativă atunci există drum de valoare maximă.

Obs. 1. Dacă în graf nu există circuite atunci există şi drum de valoare minimă şi drum de valoare maximă.

Deoarece din cele de mai sus se sesizează importanţa existenţei circuitelor într-un graf vom da în continuare un algoritm de depistare a existenţei circuitelor într-un graf:

Pasul 1. Se construieşte mulţimea A formată din nodurile pentru care toate arcele incidente sunt incidente spre interior ( noduri în care toate arcele "intră" sau, altfel spus, noduri din care nu "pleacă" nici un arc).

Pasul 2. Se găsesc toate nodurile care nu sunt din A pentru care toate arcele incidente au cealaltă extremitate în A (noduri din care se poate "ajunge" doar in A). Dacă nu există nici un astfel de arc se trece la pasul 4.

Pasul 3. Se adaugă arcele găsite la pasul 2 la mulţimea A apoi se reia algoritmul de la pasul 2, pentru noua mulţime A.

Pasul 4. Dacă A conţine mulţimea tuturor nodurilor atunci graful nu conţine circuite. Dacă au rămas noduri în afara lui A atunci graful conţine circuite.

Algoritmi de găsire a drumului optim

Din cauza varietăţii nelimitate a grafurilor posibile, nu există un algoritm care să rezolve orice problemă în timp util, dar s-au elaborat o mulţime de algoritmi, fiecare fiind cel mai eficace în anumite cazuri. Aceşti algoritmi pot fi grupaţi în cinci categorii:

1. Algoritmi prin calcul matricial (Bellman-Kalaba, I. Tomescu, Bellman-Schimbell);

2. Algoritmi prin ajustări succesive: (Ford);

3. Algoritmi prin inducţie (Dantzig);

4. Algoritmi prin ordonare prealabilă a vârfurilor grafului;

5. Algoritmi prin extindere selectivă (Dijkstra).

În continuare vom prezenta trei dintre aceşti algoritmi.

A. Algoritmul lui Bellman - Kalaba

Algoritmul se aplică în grafuri finite care nu au circuite de valoare negativă (pentru o problemă de minim) sau care nu au circuite de valoare pozitivă (într-o problemă de maxim) şi găseşte drumurile de valoare minimă (maximă) de la toate nodurile grafului la un nod oarecare, fixat. Dacă dorim să cunoaştem drumurile de valoare minimă (maximă) între oricare două noduri vom aplica algoritmul, pe rând, pentru fiecare nod al grafului.

Fie G = {x₁, x₂, ... ,x_n} un graf orientat finit. Presupunem (fără a restrânge generalitatea, că am numerotat nodurile astfel încât nodul spre care căutăm drumurile de valoare minimă (maximă) de la celelalte noduri să fie x_n.

Pasul 1. Se construieşte matricea pătratică M cu dimensiunea egală cu numărul de noduri ale grafului ale cărei elemente sunt:

m_ij =

Pasul 2. Se adaugă succesiv liniile L_i la matricea M, elementele acestora calculându-se prin relaţiile de recurenţă:

1. L_1j = m_jn j = 1,...,n (prima linie este ultima coloană, transpusă, a matricii M)

2. L_ij = min (L_i-1,j , (m_jk + L_i-1,k)) într-o problemă de minim

sau L_ij = max (L_i-1,j , (m_jk + L_i-1,k)) într-o problemă de maxim

Pasul 3. După calcularea fiecărei linii noi se compară elementele ei cu cele ale precedentei:

- Dacă L_ij = L_i-1,j pentru orice j = 1,...,n atunci se opreşte recurenţa şi ultima linie calculată conţine valorile minime ale drumurilor de la celelalte noduri la nodul x_n.

_- Dacă există cel puţin un indice j cu L_ij ¹ L_i-1,j se trece la calcularea noii linii L_i+1

Pasul 4. Pentru găsirea drumului care dă valoarea minimă de la un nod x_j la nodul x_n se găsesc, începând înapoi de la ultima linie, pe care s-au obţinut valorile finale, notată L_f, nodurile ,, ..., care formează drumul căutat, unde = x_j, = x_n şi fiecare alt indice k_i+1 este cel pentru care s-a obţinut minimul(maximul) de pe poziţia k_i al liniei L_i.

Observaţie: Pentru grafuri foarte mari, algoritmul necesită un volum mare de memorie, prin necesitatea memorării matricei M, care este greu de manipulat. Chiar dacă din cele n² arce posibile graful ar avea doar un procent foarte mic matricea grafului va avea tot n² poziţii de memorat şi analizat.

Exemplu: Presupunem dat graful orientat de mai jos, în care se doreşte găsirea drumului de valoare minimă de la nodul x₁ la nodul x₉.

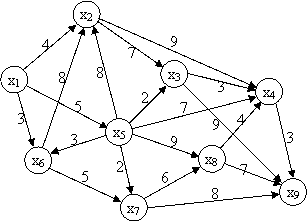
Matricea M va fi

iar după calcularea liniilor L_i obţinem:

	x1	x2	x3	x4	x5	x6	x7	x8	x9
x1	0	4	¥	¥	5	¥	¥	¥	¥
x2	¥	0	7	9	¥	¥	¥	¥	¥
x3	¥	¥	0	3	¥	¥	¥	¥	9
x4	¥	¥	¥	0	¥	¥	¥	¥	3
x5	¥	8	2	7	0	3	2	9	¥
x6	¥	8	¥	¥	¥	0	5	¥	¥
x7	¥	¥	¥	¥	¥	¥	0	6	8
x8	¥	¥	¥	4	¥	¥	¥	0	7
x9	¥	¥	¥	¥	¥	¥	¥	¥	0
L1	¥	¥	9	3	¥	¥	8	7	0
L2	¥	12	6	3	10	13	8	7	0
L3	15	12	6	3	8	13	8	7	0
L4	13	12	6	3	8	13	8	7	0
L5	13	12	6	3	8	13	8	7	0

Deoarece L₄ = L₅ oprim calcularea liniilor după calcularea liniei 5. În această linie se află valorile celor mai scurte de la toate nodurile la nodul x₉. Drumul dorit de noi (x₁ ® x₉) are valoarea dată de prima poziţie a liniei 5, fiind egal cu 13.

Pentru a găsi acest drum, plecăm înapoi de la linia 4 şi avem:

x1				x5
13	=	8	+	5		x3
		ß
		8	=	6	+	2		x4
				ß
				6	=	3	+	3
						ß
						3	®	x9

B. Algoritmul lui Ford simplificat

Algoritmul lui Ford simplificat se aplică doar în grafuri care nu admit circuite. Cu ajutorul lui se găseşte drumul de valoare optimă între două noduri fixate x_i şi x_j. Printr-o eventuală renumerotare a nodurilor putem presupune că nodul de la care porneşte drumul este x₁, care va fi numit nod iniţial, iar nodul la care se termină este x_n, numit nod final.

Algoritmul este:

Pasul 1. I se dă vârfului iniţial valoarea 0 (zero): w(x₀) = 0

Pasul 2. Se construieşte mulţimea A formată din nodul iniţial: A = {x₁}

Pasul 3. Se analizează nodurile din afara mulţimii A.

- Dacă există noduri în care se poate ajunge prin arce directe doar de la nodurile mulţimii A, acestea se adaugă la mulţimea A, cu valoarea:

w(x_i) = , în problemele de minim

sau w(x_i) = , în problemele de maxim

apoi se trece la pasul 4

- Dacă nu există nici un nod de acest tip atunci nu există nici un drum de la x₁ la x_n. STOP

Pasul 4. Se analizează mulţimea A:

- Dacă x_n Î A atunci valoarea sa reprezintă valoarea drumului de valoare optimă de la x₁ la x_n. Pentru găsirea acestui drum se porneşte înapoi de la nodul final x_n şi se găsesc nodurile ,, ..., care formează drumul căutat, unde = x_n, = x₁ şi fiecare alt indice k_i+1 este cel pentru care:

w() + v(,) = w() STOP

- Dacă x_n Ï A se reia algoritmul de la pasul 3.

Exemplu: Pentru acelaşi graf şi aceeaşi pereche de noduri din exemplul rezolvat cu algoritmul lui Bellman-Kalaba vom avea succesiv:

pas1: w(x₁) = 0

pas2: A = {x₁}

pas3: Nodurile în care se poate ajunge doar din x₁: {x₅} ¹ Æ

w{x₅) = min( w(x₁) + v(x₁,x₅)) = 0 + 5 = 5

pas4: x₉ Ï A

pas3: A = {x₁,x₅} şi nodurile în care se poate ajunge prin arce directe doar din x₁ şi x₅ sunt: {x₆}¹ Æ

w{x₆) = min( w(x₁) + v(x₁,x₆), w(x₅) + v(x₅,x₆)) = min(0 + 3 , 5 + 3) = 3

pas4: x₉ Ï A

pas3: A = {x₁,x₅,x₆} şi nodurile în care se poate ajunge prin arce directe doar din x₁, x₅ şi x₆ sunt: {x₂,x₇} ¹ Æ

w{x₂) = min( w(x₁) + v(x₁,x₂), w(x₅) + v(x₅,x₂), w(x₆) + v(x₆,x₂)) = min(0 + 4,5 + 8,3 + 8) = 4

w{x₇) = min( w(x₅) + v(x₅,x₇), w(x₆) + v(x₆,x₇)) = min(5 + 2,3 + 5) = 7

pas4: x₉ Ï A

pas3: A = {x₁,x₂,x₅,x₆,x₇} şi nodurile în care se poate ajunge prin arce directe doar din x₁, x₂, x₅, x₆ şi x₇ sunt: {x₃,x₈} ¹ Æ

w{x₃) = min( w(x₂) + v(x₂,x₃), w(x₅) + v(x₅,x₃)) = min(4 + 7,5 + 2) = 7

w{x₈) = min( w(x₅) + v(x₅,x₈), w(x₇) + v(x₇,x₈)) = min(5 + 9,7 + 6) = 13

pas4: x₉ Ï A

pas3: A = {x₁,x₂,x₃,x₅,x₆,x₇,x₈} şi nodurile în care se poate ajunge prin arce directe doar din x₁, x₂,x₃,x₅, x₆, x₇ şi x₈ sunt: {x₄} ¹ Æ

w{x₄) = min( w(x₂) + v(x₂,x₄), w(x₃) + v(x₃,x₄),w(x₅) + v(x₅,x₄), w(x₈) + v(x₈,x₄)) = min(4 + 9,7 + 3,5 + 7,13 + 4) = 10

pas4: x₉ Ï A

pas3: A = {x₁,x₂,x₃,x₄,x₅,x₆,x₇,x₈} şi nodurile în care se poate ajunge prin arce directe doar din x₁, x₂, x₃, x₄, x₅, x₆, x₇ şi x₈ sunt: {x₉} ¹ Æ

w{x₉) = min( w(x₃) + v(x₃,x₉), w(x₄) + v(x₄,x₉), w(x₇) + v(x₇,x₉), w(x₈) + v(x₈,x₉)) = min(7 + 9, 10 + 3, 7 + 8, 13 + 7) = 13

pas4: x₉ Î A şi urmează să găsim drumul care are lungimea 13.

Avem succesiv:

w(x₉) = w(x₄) + v(x₄,x₉)

w(x₄) = w(x₃) + v(x₃,x₄)

w(x₃) = w(x₅) + v(x₅,x₃)

w(x₅) = w(x₁) + v(x₁,x₅)

deci drumul căutat este: x₁ ® x₅ ® x₃ ® x₄ ® x₉

Observaţia 1. Dacă graful are un circuit atunci se poate demonstra uşor că nu vom putea da valoare nici unui nod al acestuia şi dacă există vreun drum de la x₁ la x_n care trece prin unul din nodurile circuitului nu vom putea da valoare nici lui x_n, cu toate că există drum de la x₁ la x_n.

Observaţia 2: Algoritmul necesită pentru memorare şi manipulare doar cunoaşterea, pentru fiecare nod, a nodurilor spre care "pleacă" arce din acesta şi valorile acestor arce, fiind mult mai uşor de aplicat sau implementat pe calculator. El are însă dezavantajul că se poate aplica doar în grafuri fără circuite.

C. Algoritmul Ford generalizat

Algoritmul lui Ford generalizat a fost creat cu scopul de a putea găsi drumul optim şi în grafurile care au circuite. Cu ajutorul lui se găseşte drumul de valoare optimă între două noduri fixate x_i şi x_j. Printr-o eventuală renumerotare a nodurilor putem presupune că nodul de la care porneşte drumul este x₁, care va fi numit nod iniţial, iar nodul la care se termină este x_n, numit nod final.

Algoritmul este:

Pasul 1. I se dă vârfului iniţial valoarea 0 (zero): w(x₀) = 0 şi tuturor celelalte valoarea +¥ (într-o problemă de minim) sau -¥ (într-o problemă de maxim).

Pasul 2. În ordinea crescătoare a indicilor nodurilor se calculează pentru fiecare nod, pe bază fostelor valori, noile valori cu formula:

w^*(x_i) = în problemele de minim

sau w^*(x_i) = în problemele de maxim

Pasul 3. Se compară noile valori w^*(x_i) cu fostele valori w(x_i):

- Dacă w^*(x_i) = w(x_i) pentru orice nod x_i atunci:

- dacă w(x_n) < ¥ (la problema de minim) sau w(x_n) > -¥ (la problema de maxim), valoarea nodului x_n reprezintă valoarea drumului de valoare minimă(maximă) de la x₁ la x_n. Pentru găsirea acestui drum se porneşte înapoi de la nodul final x_n şi se găsesc nodurile ,, ..., care formează drumul căutat, unde = x_n, = x₁ şi fiecare alt indice k_i+1 este cel pentru care:

w() + v(,) = w() STOP

- dacă w(x_n) = +¥ (-¥) atunci nu există nici un drum de la x₁ la x_n. STOP

- Dacă există cel puţin un nod pentru care w^*(x_i) < w(x_i) se reia algoritmul de la pasul 2 pentru noile valori ale vârfurilor.

Observaţie: Algoritmul poate găsi drumul şi în grafuri cu circuite dar este evident mult mai lent decât cel simplificat. Pentru scurtarea duratei de execuţie se poate modifica algoritmul în sensul că o valoare nou calculată a unui vârf va fi folosită imediat ca atare la calculul noilor valori ale celorlalte, nu doar după ce se calculează noile valori ale tuturor vârfurilor.

D. Algoritmul lui Dijkstra

În algoritmul Ford simplificat, pentru a găsi valoarea nodului final, deci a drumului minim, plecăm de la nodul iniţial în toate direcţiile posibile, păstrând de fiecare dată toate nodurile analizate. Acest fapt duce la un consum inutil de timp, deoarece foarte multe din aceste noduri nu vor face parte din drumul optim. Pentru a elimina acest neajuns, algoritmul lui Dijkstra încearcă să păstreze, la fiecare iteraţie, mulţimea minimă de noduri care să le conţină pe toate cele care vor forma efectiv drumul optim. În plus, algoritmul se poate aplica şi în drumuri cu circuite. Ca un minus este faptul că se aplică doar la probleme de minim. Algoritmul are următorii paşi:

Pasul 1. I se dă vârfului iniţial valoarea 0 (zero): w(x₀) = 0

Pasul 2. Se construieşte mulţimea A formată din nodul iniţial: A = {x₁}

Pasul 3. Se analizează nodurile din afara mulţimii A.

- Dacă există noduri în care se poate ajunge prin arce directe de la noduri din A (nu doar de la nodurile mulţimii A, ca la algoritmul lui Ford simplificat) se calculează pentru toate acestea:

w(x_i) = în problemele de minim

dar, spre deosebire de algoritmul lui Ford simplificat, se adaugă la mulţimea A doar cel pentru care se obţine valoarea minimă, apoi se trece la pasul 4.

- Dacă nu există nici un nod de acest tip atunci nu există nici un drum de la x₁ la x_n. STOP

Pasul 4. Se analizează mulţimea A:

- Dacă x_n Î A atunci valoarea sa reprezintă valoarea drumului de valoare optimă de la x₁ la x_n. Pentru găsirea acestui drum se porneşte înapoi de la nodul final x_n şi se găsesc nodurile ,, ..., care formează drumul căutat, unde = x_n, = x₁ şi fiecare alt indice k_i+1 este cel pentru care:

w() + v(,) = w() STOP

- Dacă x_n Ï A se reia algoritmul de la pasul 3.

Exemplu Vom aplica algoritmul la acelaşi graf folosit la ceilalţi algoritmi, pentru a putea face comparaţii:

pas1: w(x₁) = 0

pas2: A = {x₁}

pas3: Nodurile în care se poate ajunge şi din x₁: {x₂, x₅, x₆} ¹ Æ

w{x₂) = min( w(x₁) + v(x₁,x₂)) = 0 + 4 = 4

w{x₅) = min( w(x₁) + v(x₁,x₅)) = 0 + 5 = 5

w{x₆) = min( w(x₁) + v(x₁,x₆)) = 0 + 3 = 3

min(w{x₂),w{x₅),w{x₆)) = w{x₆) = 3

pas4: x₉ Ï A

pas3: A = {x₁,x₆} şi nodurile în care se poate ajunge prin arce directe din x₁ sau x₆ sunt: {x₂,x₅,x₇}¹Æ

w{x₂) = min( w(x₁) + v(x₁,x₂), w(x₆) + v(x₆,x₂)) = min(0 + 4 , 3 + 8) = 4

w{x₅) = min( w(x₁) + v(x₁,x₅)) = min(0 + 5) = 5

w{x₇) = min( w(x₆) + v(x₆,x₇)) = min(3 + 5) = 8

min(w{x₂),w{x₅),w{x₇)) = w{x₂) = 4

pas4: x₉ Ï A

pas3: A = {x₁,x₂,x₆} şi nodurile în care se poate ajunge prin arce directe din x₁, x₂ sau x₆ sunt: {x₃,x₄,x₅,x₇} ¹ Æ

w{x₃) = min( w(x₂) + v(x₂,x₃)) = min(4 + 7) = 11

w{x₄) = min( w(x₂) + v(x₂,x₄)) = min(2 + 9) = 11

w{x₅) = min( w(x₁) + v(x₁,x₅)) = min(0 + 5) = 5

w{x₇) = min( w(x₆) + v(x₆,x₇)) = min(3 + 5) = 0

min(w{x₃),w{x₄),w{x₅),w{x₇)) = w{x₅) = 5

pas4: x₉ Ï A

pas3: A = {x₁,x₂,x₅,x₆} şi nodurile în care se poate ajunge prin arce directe din x₁, x₂, x₅, x₆ şi x₇ sunt: {x₃,x₄,x₇,x₈} ¹ Æ

w{x₃) = min( w(x₂) + v(x₂,x₃), w(x₅) + v(x₅,x₃)) = min(4 + 7,5 + 2) = 7

w{x₄) = min( w(x₂) + v(x₂,x₄), w(x₅) + v(x₅,x₄)) = min(4 + 9,5 + 7) = 12

w{x₇) = min( w(x₅) + v(x₅,x₇), w(x₆) + v(x₆,x₇)) = min(5 + 2,3 + 5) = 7

w{x₈) = min( w(x₅) + v(x₅,x₈)) = min(5 + 9) = 14

min(w{x₃),w{x₄),w{x₇),w{x₈)) = w{x₃) = w{x₇) = 7

pas4: x₉ Ï A

pas3: A = {x₁,x₂,x₃,x₅,x₆,x₇} şi nodurile în care se poate ajunge prin arce directe din x₁, x₂, x₃, x₅, x₆, şi x₇ sunt: {x₄,x₈,x₉} ¹ Æ

w{x₄) = min( w(x₂) + v(x₂,x₄), w(x₃) + v(x₃,x₄),w(x₅) + v(x₅,x₄)) = min(4 + 9,7 + 3,5 + 7) =10

w{x₈) = min( w(x₅) + v(x₅,x₈), w(x₇) + v(x₇,x₈)) = min(5 + 9,7 + 6) = 13

w{x₉) = min( w(x₃) + v(x₃,x₉), w(x₇) + v(x₇,x₉)) = min(7 + 9,7 + 8) = 15

min(w{x₄),w{x₈),w{x₉)) = w{x₄) = 10

pas4: x₉ Ï A

pas3: A = {x₁,x₂,x₃,x₄,x₅,x₆,x₇} şi nodurile în care se poate ajunge prin arce directe din x₁, x₂, x₃, x₄, x₅, x₆, şi x₇ sunt: {x₈,x₉} ¹ Æ

w{x₉) = min( w(x₃) + v(x₃,x₉), w(x₄) + v(x₄,x₉), w(x₇) + v(x₇,x₉)) = min(7 + 9,10 + 3,7+8)=13

w{x₈) = min( w(x₅) + v(x₅,x₈), w(x₇) + v(x₇,x₈)) = min(5 + 9,7 + 6) = 13

min(w{x₈),w{x₉)) = w{x₈) = w{x₉) = 13

pas4: x₉ Î A şi urmează să găsim drumul care are lungimea 13.

Avem succesiv:

w(x₉) = w(x₄) + v(x₄,x₉)

w(x₄) = w(x₃) + v(x₃,x₄)

w(x₃) = w(x₅) + v(x₅,x₃)

w(x₅) = w(x₁) + v(x₁,x₅)

deci drumul căutat este: x₁ ® x₅ ® x₃ ® x₄ ® x₉

9. Reţele de transport

Într-o mare varietate de situaţii concrete din practica economică se pune problema deplasării unei cantităţi de materie, energie, informaţie etc, din anumite locuri, numite surse, în alte locuri, numite destinaţii. Pentru realizarea acestui transport se folosesc o serie de trasee, numite rute de legătură. Unităţile indivizibile ale cantităţii Q, care se deplasează de-a lungul rutelor între surse şi destinaţii, se numesc unităţi de flux, iar ansamblul rutelor, surselor, destinaţiilor şi, eventual, a altor puncte intermediare se numeşte reţea de transport.

Situaţia de mai sus poate fi reprezentată geometric printr-un graf finit, conex şi fără bucle.

Pentru ca o astfel de problemă să fie suficient de complexă pentru a necesita un studiu matematic riguros, trebuie ca fiecare sursă să poată aproviziona mai multe destinaţii şi orice destinaţie să poată fi aprovizionată de mai multe surse.

Aprovizionarea destinaţiilor se poate face direct de la surse sau prin intermediul altor puncte, numite puncte intermediare. În cazul cel mai general pot exista de asemenea legături între surse şi/sau legături între destinaţii.

Aşa cum s-a văzut şi la problema de transport, situaţia de mai sus este un cadru extrem de larg, care permite existenţa unui număr foarte mare de tipuri de probleme posibile, diferite între ele prin informaţiile suplimentare pe care le avem despre reţea şi prin obiectivele urmărite.

Una dintre acestea este problema determinării cantităţii maxime (minime) care poate fi transportată de la surse la destinaţii, în situaţia în care sursele dispun de cantităţi limitate (inferior sau superior), destinaţiile au un necesar sau o putere de absorbţie limitată inferior sau superior iar pe fiecare rută se poate transporta doar o cantitate cuprinsă între anumite limite.

Pentru studiul matematic al acestei situaţii vom da definiţiile matematice ale obiectelor implicate în problemă şi ipotezele modelului.

Definiţia 1: Se numeşte reţea de transport standard un graf finit, simplu, conex, fără bucle G = (X,U) care are următoarele proprietăţi:

1. Există şi este unic s a.î. Æ, Æ (din care doar "ies" arce), numit intrarea reţelei de transport;

2. Există şi este unic t a.î. = Æ, ¹ Æ (în care doar "intră" arce) numit ieşirea reţelei de transport;

3. S-a definit o funcţie c: U ® R⁺ care asociază fiecărui arc u un număr strict pozitiv c_u numit capacitatea arcului.

Observaţie: Este clar că exemplele obişnuite au doar rareori o singură sursă şi o singură destinaţie. Totuşi, printr-o tehnică foarte simplă, orice reţea de transport se poate aduce la forma standard:

1. Dacă sunt mai multe surse se introduce un nod suplimentar din care "pleacă" câte un arc spre fiecare sursă (şi numai spre acestea), iar capacităţile acestor arce vor fi egale cu disponibilurile surselor corespunzătoare;

2. Dacă sunt mai multe destinaţii se introduce un nod suplimentar spre care "pleacă" câte un arc din fiecare destinaţie (şi numai din acestea), iar capacităţile acestor arce vor fi egale cu necesarurile destinaţiilor corespunzătoare;

Definiţia 2: Se numeşte flux într-o reţea de transport R = (X,U) o funcţie j: U ® R⁺ care are următoarele proprietăţile:

P1. 0 £ j_u £ c_u oricare ar fi u din U; valoarea j_u se numeşte flux al arcului u

P2. oricare ar fi i ¹ s,t (suma fluxurilor arcelor care "intră" într-un nod i este egală cu suma fluxurilor arcelor care "ies" din acest nod, cu excepţia nodului iniţial şi al celui final.

Definiţia 3: Se numeşte valoare a fluxului suma fluxurilor arcelor care "pleacă" din nodul iniţial s şi se notează cu F.

Observaţie: Se poate demonstra uşor că această valoare este egală şi cu suma fluxurilor arcelor care "intră" în nodul final t. În concluzie avem:

F =

Valoarea fluxului reprezintă cantitatea care se transportă efectiv pe reţea de la surse la destinaţii.

Definiţia 4: Se numeşte flux de valoare maximă într-o reţea un flux j în această reţea, cu proprietatea că, pentru orice alt flux j' pe această reţea, avem F ³ F'.

Valoarea fluxului de valoare maximă reprezintă cea mai mare cantitate care se poate transporta efectiv pe reţea, de la surse la destinaţii.

Economic vorbind, ne interesează, referitor la o reţea, răspunsurile la următoarele întrebări:

1. Putem transporta întreaga cantitate necesară la destinaţii?

2. Dacă da, cum transportăm efectiv această cantitate de la surse la destinaţii?

3. Dacă nu, din ce motiv nu putem realiza acest transport?

4. Cum putem înlătura cu eforturi minime acest motiv?

Răspunsul la primele două întrebări se poate afla prin găsirea fluxului de valoare maximă şi compararea valorii lui cu suma necesarurilor destinaţiilor. În plus, valoarea acestuia pe un arc reprezintă cantitatea care trebuie transportată pe ruta respectivă, pentru a obţine această valoare a fluxului.

Răspunsul la ultimele două întrebări porneşte de la observaţia că cea mai mare cantitate care poate traversa reţeaua de la un cap la altul este egală cu dimensiunea celui mai îngust loc de trecere prin reţea. Dacă vrem, deci, să mărim fluxul va trebui să lărgim tocmai acest cel mai îngust loc de traversare al reţelei.

Pentru formalizarea consideraţiilor de mai sus vom introduce noţiunea de tăietură într-o reţea:

Definiţia 5: Dată o reţea de transport G(X,U) cu s = nodul iniţial şi t = nodul final, se numeşte tăietură în reţea o partiţie a mulţimii vârfurilor reţelei de transport, formată din două submulţimi V şi W (VÇW = Æ, VÈW = X) astfel încât s Î V şi t Î W.

O tăietură poate fi privită, intuitiv, ca o secţiune a reţelei, care lasă nodul iniţial cu o submulţime din noduri într-o parte, nodul final cu restul nodurilor în cealaltă parte şi retează toate arcele care trec dintr-o parte în cealaltă.

A cunoaşte o tăietură este echivalent cu a cunoaşte care sunt elementele celor două mulţimi, V şi W, care formează partiţia.

Vom nota o tăietură prin T = (V,W), convenind ca mulţimea scrisă pe prima poziţie să conţină nodul iniţial s al reţelei iar cea scrisă pe a doua, nodul final t.

Definiţia 6: Se numeşte capacitate a unei tăieturi T = (V,W) într-o reţea de transport G(X,U), notată C(T), suma capacităţilor tuturor arcelor care au extremitatea iniţială în V şi cea finală în W.

C(T) =

Pentru a nu exista nici o ambiguitate, insistăm asupra faptului că se vor lua în considerare doar arcele care trec de la mulţimea ce conţine nodul iniţial spre mulţimea care conţine nodul final, adică în sensul normal de transport (surse ® destinaţie).

Definiţia 7: Se numeşte tăietură de valoare minimă într-o reţea o tăietură T în această reţea, cu proprietatea că, pentru orice altă tăietură T' în această reţea, avem C(T) £ C(T').

Următoarele teoreme fac legătura matematică dintre fluxurile unei reţele şi tăieturile sale:

Teorema 1. Dată o tăietură T = (V,W) şi un flux j într-o reţea de transport avem:

F = –

sau, altfel spus, valoarea unui flux oarecare este egală cu suma fluxurilor arcelor care trec de la V la W din care se scade suma fluxurilor arcelor care trec invers, de la W la V, oricare ar fi tăietura T = (V,W).

Demonstraţie: Avem succesiv:

F = = + =

= + - = –

Corolar: Într-o reţea de transport valoarea oricărui flux este mai mică sau egală decât valoa-rea oricărei tăieturi.

Demonstraţie: Fie T o tăietură oarecare şi j un flux oarecare. Avem succesiv:

F = – £ £ = C(T)

Corolar: Într-o reţea de transport valoarea fluxului maxim este mai mică sau egală decât valoarea tăieturii minime.

Demonstraţia e evidentă. În plus, din cele de mai sus se vede că egalitatea are loc numai dacă, pentru tăietura minimă, există un flux pentru care toate arcele de la V la W sunt folosite la maxim (fluxul e egal cu capacitatea arcelor) iar pe toate arcele de la W la V nu se transportă nimic.

Teorema lui Ford-Fulkerson Dacă fluxul j este maximal atunci există o tăietură de capacitate egală cu valoarea fluxului.

Demonstraţie: Fie j un flux maximal. Introducem următorul procedeu de marcare a vârfurilor:

Pasul 1. Se marchează nodul iniţial s cu 0(zero);

Pasul 2. Pentru fiecare vârf marcat x_i se marchează cu:

· [+x_i] toate vârfurile nemarcate x_j pentru care există arcul (x_i,x_j) şi j(x_i,x_j) < c(x_i,x_j) (adica nodurile spre care mai e loc pentru a se transporta ceva din x_i);

· [–x_i] toate vârfurile nemarcate x_j pentru care există arcul (x_j,x_i) şi j(x_j,x_i) > 0 (adică toate nodurile spre care pleacă deja ceva din x_i);

Pasul 3. Se repetă pasul 2 până nu mai poate fi marcat nici un vârf.

Dacă vârful final t ar fi marcat, atunci începând de la acesta, am putea construi lanţul ,, ..., unde = s, = t şi marcajul oricărui vârf este +sau –. Adăugând la fluxul fiecărui arc al lanţului de tipul (,) valoarea:

D = min(,)

şi scăzând din fluxul fiecărui arc de tipul (,) aceeaşi valoare D, obţinem un flux de valoare F + D, deci fluxul j nu ar fi maximal.

În concluzie vârful t nu va fi marcat. Fie tăietura T = (V,W), unde V este formată din mulţimea nodurilor marcate iar W din cele nemarcate. În acest caz, pentru fiecare arc (x_i,x_j) care "traversează" tăietura avem:

- dacă x_i Î V atunci j(x_i,x_j) = c(x_i,x_j) deoarece nodul x_j nu e marcat

- dacă x_i Î W atunci j(x_i,x_j) = 0 deoarece nodul x_i nu e marcat

În acest caz avem:

C(T) = = – = F

şi teorema e demonstrată.

Teorema lui Ford-Fulkerson poate stabili doar valoarea fluxului maxim dar nu dă o metodă de găsire a acestuia. Pentru a rezolva problema găsirii fluxului de valoare maximă se poate folosi algoritmul lui Ford-Fulkerson.

Pentru expunerea acestuia vom introduce şi noţiunile de:

arc saturat = un arc pe care fluxul este egal cu capacitatea;

drum complet = un drum de la nodul iniţial s la nodul final t care conţine cel puţin un arc saturat;

flux complet = un flux pentru care orice drum de la nodul iniţial s la nodul final t este complet.

Algoritmul lui Ford-Fulkerson

ETAPA I Se determină un flux complet.

Pasul 1. Se numerotează nodurile reţelei de transport astfel încât x₁ = s şi x_n = t;

Pasul 2. Se asociază grafului fluxul nul (j_u = 0 pentru orice arc u din graf);

Pasul 3. În ordine lexicografică, se ia pe rând fiecare drum D de la nodul iniţial la cel final, se calculează valoarea D_D = şi se adaugă la fluxul de pe fiecare arc al drumului. Arcul(arcele) unui drum D pentru care s-a obţinut valoarea minimă D_D va fi după această adăugare, în mod evident, saturat şi deci drumul D va fi complet.

După epuizarea tuturor drumurilor se obţine un flux complet, de valoare F = . Deoarece alegerea drumurilor în ordine lexicografică nu ţine cont de structura reţelei, aşa cum se poate vedea pe un exemplu, acest procedeu nu asigură întotdeauna găsirea fluxului maxim. Acest impediment poate fi depăşit fie prin găsirea unei ordini de parcurgere a tuturor drumurilor, care să dea pentru fiecare reţea fluxul maxim, în urma procedeului de mai sus, fie prin redistribuirea judicioasă a fluxului găsit la etapa I. A doua variantă este cea care se aplică la etapa II.

ETAPA II Se determină fluxul maxim

Pasul 4. Se marchează nodul iniţial s cu 0(zero);

Pasul 5. Pentru fiecare vârf marcat x_i se marchează cu:

· [+x_i] toate vârfurile nemarcate x_j pentru care există arcul (x_i,x_j) şi j(x_i,x_j) < c(x_i,x_j) (adica nodurile spre care mai e loc pentru a se transporta ceva din x_i);

· [–x_i] toate vârfurile nemarcate x_j pentru care există arcul (x_j,x_i) şi j(x_j,x_i) > 0 (adică toate nodurile spre care pleacă deja ceva din x_i);

Pasul 6. Se repetă pasul 5 până este marcat nodul final sau până când nu mai poate fi marcat nici un vârf;

Pasul 7. Dacă nodul final a fost marcat atunci fluxul este maxim şi algoritmul se opreşte, în caz contrar trecându-se la pasul 8;

Pasul 8. Construim un lanţul L = ,, ..., unde = s, = t şi marcajul oricărui vârf este +sau –. Se calculează:

D_L = min(,)

care se adaugă la fluxul fiecărui arc al lanţului de tipul (,) şi se scade din fluxul fiecărui arc de tipul (,).

Pasul 9. Se şterge marcajul şi se reia algoritmul de la pasul 4.

În final, tăietura de valoare minimă este cea în care V = mulţimea nodurilor marcate iar W = mulţimea nodurilor nemarcate.

Observaţia 1. Algoritmul nu asigură întotdeauna găsirea fluxului maxim, deoarece se poate ca creşterea fluxului la fiecare iteraţie să se facă cu cantităţi din ce în ce mai mici astfel încât suma lor să nu atingă niciodată marginea superioară dată de valoarea tăieturii minime, algoritmul având o infinitate de paşi. Teorema de mai jos dă o condiţie suficientă pentru ca algoritmul să se termine într-un număr finit de paşi:

Teoremă Dacă toate capacităţile rutelor reţelei sunt numere raţionale atunci algoritmul lui Ford-Fulkerson are un număr finit de paşi.

Demonstraţie Prin înmulţirea tuturor acestor capacităţi cu cel mai mic multiplu comun al numitorilor se obţine o reţea cu toate capacităţile numere naturale. Ţinând cont de formula de calcul, la fiecare iteraţie cantitatea adăugată D va fi număr natural şi cum valoarea fluxului maxim este mărginită de capacitatea tăieturii minime C_min, care este de asemenea număr natural, algoritmul va avea nevoie de cel mult C_min paşi pentru a o atinge.

Observaţia 2. Teorema de mai sus asigură doar o limitare superioară a numărului de iteraţii ale algoritmului, faţă de capacitatea tăieturii minime. Această valoare poate fi însă, în anumite cazuri, foarte mare şi, dacă nu se iau precauţii suplimentare, algoritmul nu va da soluţia în timp util. Depăşirea acestei situaţii este asigurată de următoarea teoremă:

Teoremă Dacă la fiecare iteraţie se alege drumul (lanţul) de lungime minimă atunci algoritmul va avea cel mult ×m×n iteraţii, unde n = numărul de noduri iar m = numărul de muchii.

Observaţia 3. Există probleme în care se doreşte găsirea fluxului minim într-o reţea, valorile fluxului pe arce fiind limitate inferior de capacităţile acestora. În acest caz se aplică de asemenea algoritmul lui Ford-Fulkerson astfel:

Pasul 1. Se calculează M = maximul capacităţilor arcelor

Pasul 2. Se construieşte reţeaua R', care este fosta reţea, în care au fost modificate doar capacităţile arcelor, acestea devenind = M – c_u

Pasul 3. Se găseşte cu algoritmul Ford-Fulkerson fluxul j, de valoare maximă, în această reţea

Pasul 4. Fluxul de valoare minimă în reţeaua iniţială va avea valorile j' = M – j

Observaţia 4. Există şi alte tipuri de probleme asemănătoare celor de mai sus. Astfel, se poate pune problema:

- găsirii capacităţilor minime ale arcelor cu care se poate asigura transportarea întregii cantităţi de la surse la destinaţii

- fluxului minim(maxim) într-o reţea în care capacităţile rutelor sunt limitate atât superior cât şi inferior;

- În cazul în care rutelor li se asociază şi costuri unitare de parcurgere, putem căuta fluxul maxim de cost minim;