Modelul Lesourne-Leban
Asemănarea cu modelul Jorgenson: orizontul de timp este infinit.
Deosebiri:
- vizează schimbări în structura financiară (finanţarea poate fi făcută din acţiuni sau din credite);
- criteriul de optim: maximizarea valorii firmei ca sumă actualizată de dividende;
- ţine seama de politica de taxare (impozitare a guvernului).
Ecuaţiile modelului:
- ecuaţia de balanţă care formalizează sursele de finanţare a bunurilor capital:
![]() (1)
(1)
unde:
X(t) – valoarea acţiunilor (capitalul social al firmei)
Y(t) – împrumuturi (credite)
K(t) – valoarea bunurilor capital.
- ecuaţia de evoluţie a bunurilor capital (investiţia netă); este ecuaţia de stare:
![]() (2)
(2)
unde
I(t) – investiţia brută;
a – rata de amortizare;
![]() - investiţia netă.
- investiţia netă.
- Ecuaţia profitului net
![]() (3)
(3)
unde:
E(t) – profitul net al firmei;
f – rata de impozitare;
R(Q(t)) – veniturile firmei (din vânzări);
w – salariul pe persoană ocupată;
L(t) – personalul ocupat;
![]() - creşterea capitalului social;
- creşterea capitalului social;
D(t) – valoarea dividendelor.
Ecuaţia (3) cuprinde modul de
distribuire şi modul de formare a profitului net: ![]() (distribuirea
profitului net pentru dividende şi/sau creşterea capitalului social(acumulări)).
(distribuirea
profitului net pentru dividende şi/sau creşterea capitalului social(acumulări)).
Mecanismul de formare a profitului net este:
![]()
Observaţie: Spre deosebire de modelul Jorgenson, cheltuielile cu capitalul se consideră valoarea amortizărilor (la Jorgenson costul capitalului era exprimat ca o pondere din investiţia brută). Ca şi în modelul amintit, se consideră două inputuri: capitalul şi forţa de muncă.
Ipoteze asupra funcţiei de venit (venituri din vânzări)
- R(Q(t)) este strict concavă:
![]()
-
R(Q(t)) este monoton strict crescătoare: ![]()
-
veniturile marginale la scala de
fabricaţie sunt strict descrescătoare: ![]()
Performanţa modelului: firma este condusă de acţionari, criteriul este maximizarea fluxurilor de dividende pe un orizont infinit.
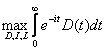 (4)
(4)
Restricţii asupra dividendelor
Dividendele sunt nenegative:
![]() (5)
(5)
Restricţii de limitare a valorii împrumutului:
![]() (6)
(6)
unde k este ponderea maximă a datoriilor (creditelor bancare) în raport cu valoarea capitalului social.
Din ecuaţia de balanţă rezultă Y(t) = K(t) – X(t). înlocuim în (6):
![]() (6’)
(6’)
Limitele artificiale pentru variabilele de control (dividende şi investiţii):
![]() (7)
(7)
![]() (8)
(8)
(necesare pentru a obţine un domeniu închis al variabilelor de control).
Modelul
matematic (Lesourne şi Leban) este:
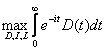 (9)
(9)
![]() (10)
(10)
Observaţie: în ecuaţia (3) am ţinut seama de ecuaţia de balanţă:
![]()
![]() (11)
(11)
![]() (12)
(12)
![]() restricţii
momentane asupra variabilelor de comandă
restricţii
momentane asupra variabilelor de comandă
Pentru rezolvare aplicăm principiul lui Pontreaghin:
Hamiltonianul problemei:
![]() (15)
(15)
Lagrangeanul problemei:
![]()
![]() (16)
(16)
Presupunem, din raţiuni economice, că:
![]()
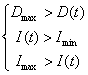
Condiţiile de optim ale modelului sunt:
![]() (17)
(17)
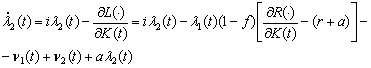 (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
Din (19) şi (25) rezultă că:
![]() (26)
(26)
din (21) şi (26):
![]() (27)
(27)
(venitul marginal al muncii este egal cu costul marginal).
Conform (20)![]() relaţia (18) devine:
relaţia (18) devine:
![]() (28)
(28)
Traiectorii
posibile
|
TR. nr. |
|
|
|
|
1 |
0 |
+ |
0 |
|
2 |
0 |
0 |
+ |
|
3 |
0 |
0 |
0 |
|
4 |
+ |
+ |
0 |
|
5 |
+ |
0 |
+ |
|
6 |
+ |
0 |
0 |
Transformarea condiţiilor de
optim pe traiectoriile 1, 2, 3 pentru care ![]() : (19)
: (19)![]() (17) devine:
(17) devine:
![]() (29)
(29)
Pe traiectoriile 1, 2, 3, (28) devine:
![]() (30)
(30)
Ipoteză: ![]() : revenirea acţionarilor este diferită de costul unitar al împrumutului.
: revenirea acţionarilor este diferită de costul unitar al împrumutului.
i – rata de revenire a acţionarilor la o unitate monetară investită pe acţiuni;
(1 – f)r – costul împrumutului (partea dintr-o unitate monetară de profit net care constituie restituirea datoriilor).
Analiza
traiectoriilor de bază
Traiectoria 1: ![]()
![]()
Din (29) rezultă:
![]() (31)
(31)
deci acţiunile sunt mai ieftine decât creditul şi este raţional ca finanţarea să se facă din acţiuni.
Din (30) rezultă:
![]() (32)
(32)
înlocuim pe ![]() din (31) în (32):
din (31) în (32):
![]() (33)
(33)
şi notăm cu ![]() soluţia
acestei ecuaţii (valoarea staţionară când finanţarea se face numai din acţiuni).
soluţia
acestei ecuaţii (valoarea staţionară când finanţarea se face numai din acţiuni).
Traiectoria 2: ![]()
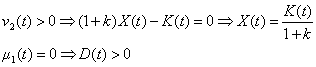
Din (29) rezultă:
![]()
adică:
![]() (35)
(35)
Deoarece ![]() rezultă că
acţiunile sunt scumpe şi creditele sunt ieftine; deci finanţarea se va
face din credite.
rezultă că
acţiunile sunt scumpe şi creditele sunt ieftine; deci finanţarea se va
face din credite.
Din (30) rezultă:
![]() (36)
(36)
înlocuim pe ![]() din (35) şi
obţinem:
din (35) şi
obţinem:
![]() (37)
(37)
Notăm cu ![]() soluţia
acestei ecuaţii (valoarea staţionară când finanţarea se face din credite la maxim).
soluţia
acestei ecuaţii (valoarea staţionară când finanţarea se face din credite la maxim).
Traiectoria 3: ![]()
Din (29) rezultă:
![]()
situaţie exclusă prin ipoteză, deci traiectoria 3 nu este admisibilă.
Traiectoria 4: ![]()
Din (24) rezultă:
![]()
deci finanţarea se face numai din acţiuni.
Din (29)![]()
![]() pentru că
pentru că ![]() .
.
Din (30), pentru ![]() , avem:
, avem:
![]()
Înlocuim ![]() din ecuaţia
precedentă şi ţinând cont că i < (1 – f)r, va rezulta:
din ecuaţia
precedentă şi ţinând cont că i < (1 – f)r, va rezulta:
![]()
Traiectoria 5: ![]()
Din (24) rezultă:
![]()
deci finanţarea este mixtă (din acţiuni şi credite la maxim).
Din (30), pentru ![]() , avem:
, avem:
![]()
unde ![]() este soluţia
staţionară în cazul finanţării mixte.
este soluţia
staţionară în cazul finanţării mixte.
Traiectoria 6: ![]()
Din (23) rezultă:
![]()
iar din (24) avem:
![]()
rezultând că:
![]()
Din (30), pentru ![]() , avem:
, avem:
![]()
unde ![]() este soluţia
staţionară în cazul finanţării mixte.
este soluţia
staţionară în cazul finanţării mixte.
Analiza
soluţiei
Traiectoriile 4,5,6 nu pot fi traiectorii
finale, întrucât nu poate fi optimal să nu se plătească
dividende pe termen lung (deoarece ![]() ); deci traiectoriile 1 şi 2 sunt singurele traiectorii
finale.
); deci traiectoriile 1 şi 2 sunt singurele traiectorii
finale.
Traiectorii
într-un singur stadiu
a)
dacă ![]() şi
şi ![]() , traiectoria optimă este traiectoria 1.
, traiectoria optimă este traiectoria 1.

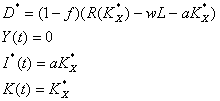
b)
dacă ![]() şi
şi ![]() , traiectoria optimă este traiectoria 2.
, traiectoria optimă este traiectoria 2.

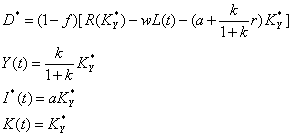
Traiectorii
în două faze
Sunt formate din cuplarea traiectoriilor 4, 5 şi 6, înaintea traiectoriei 1 sau 2.
întrucât modelul are restricţii pure asupra stării, trebuie să considerăm posibilitatea ca variabilele adjuncte să nu fie continue.
în punctul τ în care λ(t) este discontinuă, trebuie satisfăcute relaţiile:
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
întrucât ![]() , din (42) rezultă:
, din (42) rezultă:
![]() (46)
(46)
Din (45) şi (46) rezultă ![]() deci
deci ![]() este continuă.
este continuă.
Din (19) rezultă![]() deci
deci ![]() este continuă.
este continuă.
Întrucât pe traiectoriile 1 şi 2 m1(t) = 0, este necesar ca
traiectoriile care preced traiectoriile 1 sau 2 să verifice ![]() . Rezultă că în punctul de comutaţie:
. Rezultă că în punctul de comutaţie:
![]()
Cum ![]() fiindcă
fiindcă ![]() , înlocuind în (17) obţinem:
, înlocuind în (17) obţinem:
![]() (47)
(47)
Pe traiectoria 4 avem ![]() .
.
înlocuim în (47) relaţiile: ![]() şi rezultă:
şi rezultă:
![]()
Din condiţia de optim (28), prin explicitarea
lui ![]() rezultă:
rezultă:
![]()
şi înlocuind pe ![]() în (47), ţinând
seama că
în (47), ţinând
seama că ![]() , avem:
, avem:
![]()
![]()
Am determinat deja că ![]() .
.
Obţinem:
Dacă ![]() , traiectoria de magistrală este:
, traiectoria de magistrală este:
Tr4 → Tr1.
|
TR4 |
TR1 |
|
|
|
|
|
valoare staţionară |
|
|
|
|
|
|
t
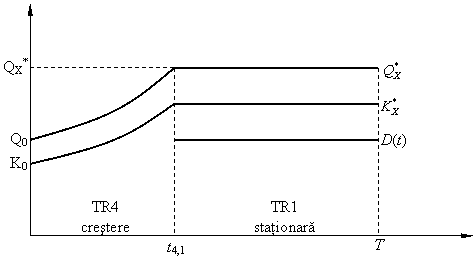
Traiectoria de magistrală TR4 → TR1 este cazul finanţării pure din acţiuni.
Pe Traiectoria 5, ![]() .
.
Din condiţia de optim (28) rezultă
prin explicitarea lui ![]() :
:
![]()
şi înlocuind pe ![]() în (47), ţinând
seama că
în (47), ţinând
seama că ![]() :
:
![]()
![]()
Traiectoria 5 trebuie conectată cu traiectoria 2 şi va rezulta cazul finanţării maxime din împrumut.
Obţinem:
Dacă:
![]() şi
şi ![]()
traiectoria de magistrală este TR5 → TR2.
|
TR5 |
TR2 |
|
|
|
|
|
traiectorie staţionară |
|
|
|
|
|
|
în cazul acestei magistrale, creşterea se va face cu finanţare maximă din împrumut.
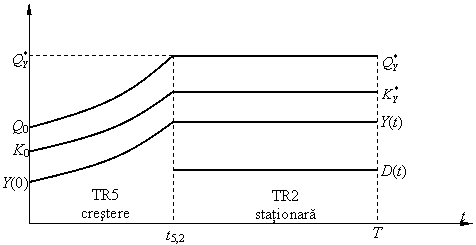
Traiectoria 6 nu poate precede traiectoria 1 sau 2, datorită continuităţii lui K(t).
Pe traiectoria 1: ![]()
Pe traiectoria 6: ![]()
Pe traiectoria 2: ![]() .
.
Deci traiectoriile în două stadii sunt:
TR4→TR1
TR5→TR2
Traiectoriile în mai multe stadii:
a)
dacă ![]() şi
şi ![]() , traiectoria optimală este:
, traiectoria optimală este:
TR5 → TR6 → TR4 → TR1
b)
dacă ![]() şi
şi ![]() , traiectoria optimală este:
, traiectoria optimală este:
TR5 → TR2